高校数学においても,「構造・存在・構成」という考え方が基礎にある.「構造・存在・構成」は19世紀の後半に西洋文明のなかで自覚的につかまれ,20世紀になって数学だけではなく,自然科学,言語学や社会科学など,およそ科学といわれる分野において一般的になった考え方である.人が何かを解明しようとするときとる普遍的な考え方である.
そのことを1次不定方程式で考えよう.
![]() と
と![]() を未知数とする
を未知数とする![]() のような方程式を不定方程式という.この場合は
のような方程式を不定方程式という.この場合は![]() と
と![]() の次数は1なので「1次不定方程式」という.どうして「不定」なのか.式
の次数は1なので「1次不定方程式」という.どうして「不定」なのか.式![]() は座標平面では直線を表し,直線上の点の
は座標平面では直線を表し,直線上の点の![]() 座標の値はすべてこの方程式を満たす.つまり,未知数の数(この場合は2個)より方程式の数(この場合は1個)が少なく,解は無数にあって定まらないので「不定」と言う.
座標の値はすべてこの方程式を満たす.つまり,未知数の数(この場合は2個)より方程式の数(この場合は1個)が少なく,解は無数にあって定まらないので「不定」と言う.
![]() と
と![]() が互いに素な整数であるとき,
一次不定方程式
が互いに素な整数であるとき,
一次不定方程式![]() に関して,次の問いに答よ.
に関して,次の問いに答よ.
解答
逆に任意の整数![]() を用いて
を用いて
だから,![]() のすべての解はあるひと組の解
のすべての解はあるひと組の解![]() と整数
と整数![]() を用いて
を用いて
これは解の全体を![]() 平面上に置くとき,
直線
平面上に置くとき,
直線![]() 上に等間隔に並んでいることを意味している.
上に等間隔に並んでいることを意味している.
任意の![]() の要素
の要素![]() をとり,それを
をとり,それを![]() で割る.商が
で割る.商が![]() ,余りが
,余りが![]() であるとする.
であるとする.
一方
![]() と
と![]() が互いに素なら
が互いに素なら![]() と
と![]() も互いに素であるから,
こうして解が係数のより小さいものの解から構成できる.
この過程を繰り返すと,最後は一方は
も互いに素であるから,
こうして解が係数のより小さいものの解から構成できる.
この過程を繰り返すと,最後は一方は![]() となる.
となる.
![]() または
または![]() の解として
の解として![]() か
か![]() がとれる.
ここから逆に戻っていけば
がとれる.
ここから逆に戻っていけば![]() の解が得られる.
の解が得られる.
これが1次不定方程式の基本的な事実である.
(1)が1次不定方程式の解の構造を問うている.「構造」という言葉は訓読みすれば「つくりとかまえ」である.ものの内部のつくられかたと,そのものの現れかたを意味する.「社会構造」や「言語構造」などのように「構造」としてとらえるためには,考えている全体,という意識がなければならない.この全体という意識,考え方自体は近代が生み出したものであり,「構造」は近代になって用いられるようになった.そのさきがけは,次の二例である.
◇『小説神髄』(坪内逍遙)「いくらかはじめに土台をまうけてさて構造(カウゾウ)に着手せざれば」/ここでは「つくり」が主になっている.土台は構造に含まれていない.
◇『流行』(森鴎外)「此家は今日に見えている周囲の構造(コウザウ)が寺らしくても,寺ではない」/ここでは「かまえ」が主になっている.
このように数学は,考える対象を集合としてとらえ,その集合がどのような構造をもっているのか,それを考える.
だがさらに,考えている対象が本当に実質的な内容をもつのか,ということが問題である.(1)の![]() は存在するのか.条件を満たす集合の要素は「存在」しているのか.
は存在するのか.条件を満たす集合の要素は「存在」しているのか.
そしてさらに,その要素を具体的につかむことができるのか,つまり一般的な「構成」方法はあるのか,が問題になる.
つまり考える対象としての集合が明確に定まったとしてそのうえで,
構造は,存在と構成とあわせて考えるときはじめてその集合を解明したといえる.実は高校数学はすべてこのような「構造・存在・構成」を調べ,学ぶこととしてとらえることが出来る.
解答
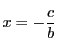 で1個.
で1個.
![]() のとき.方程式を変形して
のとき.方程式を変形して
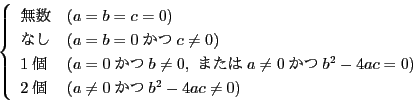
![]() の場合にも解の構成方法が存在し,
それをまとめたものがいわゆる2次方程式の解の公式である.
それを解答のなかで用いている.
の場合にも解の構成方法が存在し,
それをまとめたものがいわゆる2次方程式の解の公式である.
それを解答のなかで用いている.
さらに,すべての3次方程式,4次方程式の解を構成する方法がある.つまり,3次方程式,4次方程式の解の公式が存在する.
18世紀から19世紀,5次方程式の解の公式を作ろうと多くの人が努力した.しかし出来なかった.ついに,アーベルとガロアによって,5次方程式には解の公式が存在しないことが証明された.
解はつねに存在する.しかしそれを求める一般的な方法はない.
ここでこのような集合とその構造に関する入試問題を紹介しよう.
0でない複素数からなる集合 ![]() は次を満たしているとする.
は次を満たしているとする.
解答
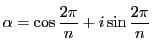 とおく.
とおく.
![]() の任意の2つの要素
の任意の2つの要素
![]() に対して
に対して
![]() も明らかに
も明らかに ![]() の解なので,再び
の解なので,再び ![]() の要素である.
の要素である.
よって ![]() は題意を満たすちょうど
は題意を満たすちょうど ![]() 個の複素数からなる集合である.
個の複素数からなる集合である.
![]() で
で ![]() なら
なら
![]() なので
なので![]() である.つまり
である.つまり
![]() なら
なら ![]() である.
である.
![]() の要素
の要素 ![]() の偏角
の偏角 ![]() は
は
![]() でとるとする.
でとるとする.
![]() の要素で偏角が正で最小であるものを
の要素で偏角が正で最小であるものを ![]() とする.
とする.
![]() の任意の要素
の任意の要素 ![]() をとる.
をとる.
このとき
![]() であるが
であるが
もし
![]() なら偏角が正で
なら偏角が正で ![]() の偏角より小さい
要素
の偏角より小さい
要素 ![]() が存在し,
が存在し,![]() の要素で偏角が正で最小であるものを
の要素で偏角が正で最小であるものを ![]() としたことと矛盾する.
としたことと矛盾する.
ゆえに
![]() .つまり
.つまり ![]()
ゆえに ![]() の要素はすべて
の要素はすべて ![]() のべきである.
のべきである.
![]() のべきで初めて1になるものを
のべきで初めて1になるものを ![]() とすれば
とすれば
別解
![]() とする.
とする.
![]() の任意の要素
の任意の要素![]() をとる.条件から
をとる.条件から
![]() に対して
に対して
![]() なので,
なので,
構造・存在・構成はすべて命題として記述され,その成立が証明されてはじめて事実として確定する.
式や文章で表された事柄で,正しいか正しくないかが明確に決まるものを命題という.命題が正しいことを真であるといい,正しくないことを偽であるという.
「事柄」そのものは定義されていないが,数学的現象について何らかの事実や推論を述べたもの,と言うことである.「5は3より大きい」は命題である.「5は3より美しい」は命題ではない.なぜなら「3より大きい」は明確に定義されるが,「3より美しい」は定義されないからである,としてよい.
「正しいか正しくないかが,明確に決まる」かどうかどうやって判断するのだろう.証明できるか反例があげられたとき真偽が決定される.とすれば,証明もできないし反例もあげられないとき,それは命題ではないのか,あるいは力不足で証明もできないし反例もあげられないだけであるのか,どうやって判断するのかということである. 証明もせず反例もあげないで,あらかじめ「命題」であるかどうか判断できるのだろうか.
さらに次のような問題もある.正しいか正しくないかはつねに決定されるのか,ということである.命題は真偽いずれかであるとしても,決定はできるのか.実はこの問題は数学体系の完備性,十分性という問題で,大変難しい.
これらはすべて当然で自然な疑問である.だが,この問題を掘りさげようと思ったら,数学基礎論の勉強をしなければならない.いずれも数学体系をどのように組み立てるのかという難しい問題なのだ.高校の教科書の定義は厳密な意味で「命題」の定義ではない.実は命題とは「いくつかの公理と論理演算の列」として定義されるのだが,ここではそれ以上追求することはできない.
このように高校数学のなかには,論理的な穴がいっぱいある.それはそれでいいのだ.それは人間が数学的現象を捉えるときの不十分さということであり,さらに学ぶなかで必要なときに解決していけばいいのだ.もし上に書いたようなことが気になる人はさらに勉強を続けてほしい.
「命題」はわかったものとし,これを基本にして順次考えていこう.「16は4の倍数である」は命題である.この16を変数 ![]() に変えた「
に変えた「 ![]() は4の倍数である」は
は4の倍数である」は![]() に何が入るのかによって真になったり偽になったりする.この場合は16を
に何が入るのかによって真になったり偽になったりする.この場合は16を![]() に置きかえたが文字は必要に応じて使い分ける.
に置きかえたが文字は必要に応じて使い分ける.
命題の主部を適当な変数,例えば ![]() や
や![]() などに置きかえたものを命題関数という.そしてこれを
などに置きかえたものを命題関数という.そしてこれを ![]() や,変数を明確にしたいときは
や,変数を明確にしたいときは ![]() のように書く.例えば
のように書く.例えば ![]() :「
:「![]() は奇数である」のようなものだ.命題関数
は奇数である」のようなものだ.命題関数 ![]() はそれ自体真偽が定まらないから命題ではない.
はそれ自体真偽が定まらないから命題ではない. ![]() に値を代入することによって命題になる.「真である」ことを「成立する」ともいう.
に値を代入することによって命題になる.「真である」ことを「成立する」ともいう.
この![]() についていえば,
についていえば,![]() つまり「3 は奇数である」は真,
つまり「3 は奇数である」は真,![]() つまり「4 は奇数である」は偽である.命題関数というからには何かの値をとると考えることもできる.この場合の値は何かといえば,それは「真」と「偽」だこの二つの値をとる.だから上の例では
つまり「4 は奇数である」は偽である.命題関数というからには何かの値をとると考えることもできる.この場合の値は何かといえば,それは「真」と「偽」だこの二つの値をとる.だから上の例では
![]() と考えることもできる.
と考えることもできる.
そこで「条件」の定義だが,命題関数 ![]() のことを
のことを![]() に関する条件というのだ.命題の定義にたちかえっていうと,文字を
に関する条件というのだ.命題の定義にたちかえっていうと,文字を ![]() とすれば,条件とは「
とすれば,条件とは「![]() に代入することによって真偽が定まる式や文」のことである.何となく使ってきた「条件」もこのようにして明確に定義される.
に代入することによって真偽が定まる式や文」のことである.何となく使ってきた「条件」もこのようにして明確に定義される.
実数は,文字に対し 2次方程式
は実数根をもつ.
となる.一方,文字:「
は実根をもつ.」
とおく.すると,:
は
を満たす.
命題関数のいずれもが成り立つ.このようなとき,2つの条件は,
を満たすなら真である.
命題関数は,
を満たすなら真である.
なお,条件は単に![]() のように変数を明示しないで書くことも多い.
のように変数を明示しないで書くことも多い.
これに対して,二つの条件![]() を用いて
を用いて
![]() と表される推論も命題である.推論型の命題を複合型命題ということもある.ここで
と表される推論も命題である.推論型の命題を複合型命題ということもある.ここで![]() や
や![]() は例えば
は例えば
のような何かの条件である.この例の場合:
は
をみたす.
:
は
をみたす.
このように命題には事実を述べた断定型と,推論を述べた推論型がある.しかし「3は奇数である」という断定型命題は,「![]() が3ならば
が3ならば![]() は奇数である」と推論型に表されるので,基本的に命題は推論型であるとしてもよい.
は奇数である」と推論型に表されるので,基本的に命題は推論型であるとしてもよい.
条件の形に表される命題を考えよう.このとき 条件が成立するならば,条件
が成立する. (これを「
」と記す).
いわば,複合命題をさらに細かく分けて, 各段階の成立が明白となるようにすることである.
その道筋を見つけることが,証明の根幹である.
だから問題解決の第一歩は,次のことを確認することである.
このように問題を読んだらまず問題を分析し,どのような条件が成立すると仮定するとき,何を決定しなければならないのかを明確にすることである.
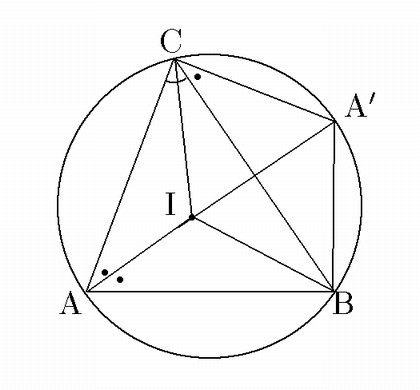
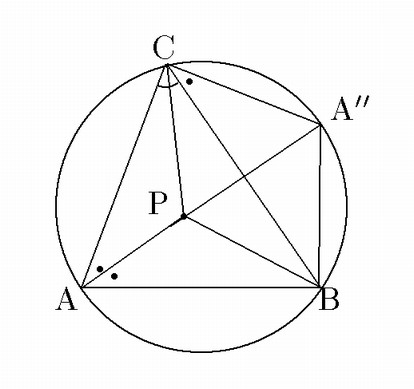
平面上の鋭角三角形
![]() の内部(辺や頂点は含まない)に点Pをとり,
の内部(辺や頂点は含まない)に点Pをとり,
![]() をB,C,Pを通る円の中心,
をB,C,Pを通る円の中心,
![]() をC,A,Pを通る円の中心,
をC,A,Pを通る円の中心,
![]() をA,B,Pを通る円の中心とする.
このときA,B,C,
をA,B,Pを通る円の中心とする.
このときA,B,C,
![]() が同一円周上にあるための
必要十分条件はPが
が同一円周上にあるための
必要十分条件はPが
![]() の内心に一致することであることを示せ.
の内心に一致することであることを示せ.
考え方
全体に共通な前提:
平面上の鋭角三角形の内部(辺や頂点は含まない)に点Pをとり,
をB,C,Pを通る円の中心,
をC,A,Pを通る円の中心,
をA,B,Pを通る円の中心とする.
このもとで,二つの命題:
甲:A,B,C,に対し「甲ならば乙」,「乙ならば甲」のいずれもが成り立つことを示す. これが問題の構造である.が同一円周上にある.
乙:Pがの内心に一致する.
そのうえで証明法であるが,次のような間接証明ができないか考えてみよう.
1) 条件を満たすものは一つしかない. 2)
も
も条件
を満たす.
3) ゆえにである.
中心が同一直線上にない三円が同一の点を共有すれば, その点は一つしかない.あるいは,三角形の外心はただ一つしかない. この簡単なことを用いると比較的簡明に証明できる.
証明
点![]() と
と
![]() が題意のように定まっている
前提のもとで次の二条件の同値性を示す.
が題意のように定まっている
前提のもとで次の二条件の同値性を示す.
条件甲:A,B,C,
![]() が同一円周上にある.
が同一円周上にある.
条件乙:Pが
![]() の内心
の内心![]() と一致する.
と一致する.
(1) 甲ならば乙を示す.
|
|
ここで
角の二等分より
この結果
|
三点
![]() を中心とする三円上に
を中心とする三円上に![]() と
と![]() の両点がある.
これら三円の中心が一直線上に来ることはない.
よって三円が共有する点は一点しかない.
つまり
の両点がある.
これら三円の中心が一直線上に来ることはない.
よって三円が共有する点は一点しかない.
つまり
![]() である.
である.
(2) 乙ならば甲を示す.
|
つまり |
|
では次の問題はどうだろうか.
![]() を0でない3つの実数とする.
を0でない3つの実数とする.
![]() ,
,![]() ,
,![]() とおき,
以下の命題を考える.
とおき,
以下の命題を考える.
こうなると問題の分析が難しい.(2)は前提が ![]() である.そのもとでの
である.そのもとでの![]() の成立を示せといっている.このところをおさえることと,命題の否定の作り方を正しくすること.これに注意して解いてみてほしい.
の成立を示せといっている.このところをおさえることと,命題の否定の作り方を正しくすること.これに注意して解いてみてほしい.
解答
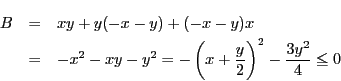
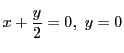 ,つまり
,つまり
(![]() )の対偶は,「
)の対偶は,「![]() かつ
かつ![]() であるとき,
であるとき,
![]() の正の個数は0,2,3である」である.
の正の個数は0,2,3である」である.
もし![]() なら(1)から
なら(1)から![]() なので,
なので,![]() .よって
.よって![]() である.
である.
![]() なら(
なら(![]() )から
)から![]() の正の個数は3.
の正の個数は3.
![]() なら
なら![]() の正の個数0か2.
の正の個数0か2.
よって(![]() )の対偶が示された.
)の対偶が示された.
![]() ,
,![]() とする.
とする.
![]() より
より![]() である.
である.![]() なので
なので
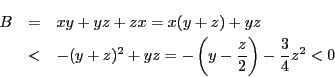
よって![]() のなかの負のものは0個,つまりすべて正である.
□
のなかの負のものは0個,つまりすべて正である.
□