

 次: 4章解答
上: 問題と考え方
前: 問題
次: 4章解答
上: 問題と考え方
前: 問題
1.1
[98中京大]
問題
1.1
解答
1.1
軌跡は媒介変数の存在条件である.
この観点からいくつかの解法を考えておこう.
基本は連立1次方程式を解くように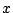 と
と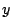 を
を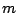 で表すことである.
そこからとりうる範囲を確定して,
で表すことである.
そこからとりうる範囲を確定して,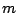 を消去すればよい.
を消去すればよい.
1.2
[98奈良女子大]
問題
1.2
解答
1.2
反転の応用形である.
反転の場合と同様に
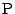 と
と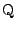 は互いに他を表すことができる.
は互いに他を表すことができる.
1.3
[01北大]
問題
1.3
解答
1.3
(1)は図形的に反転の関係を求めてから,一方を他方で表してもよいし,
また直線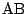 の方程式を求め,直線
の方程式を求め,直線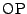 との交点として
との交点として
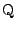 を確定してもよい.
を確定してもよい.
1.4
[99都立大]
問題
1.4
解答
1.4
一見見かけは複雑だが,
逆に解ければ条件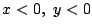 に代入するだけである.
分母が0となるときを別に考え,
分母を払えば
に代入するだけである.
分母が0となるときを別に考え,
分母を払えば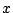 と
と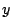 の連立1次方程式である.
の連立1次方程式である.
1.6
[97東大文系]
問題
1.6
解答
1.6
直線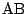 を
を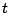 を用いて表すと簡単な式になった.
ただし3次式である.しかし
を用いて表すと簡単な式になった.
ただし3次式である.しかし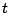 の3次方程式と見て
解が与えられた範囲にあることが,必要十分条件であることは変わりない.
3次関数なので極値の位置で場合分けである.
の3次方程式と見て
解が与えられた範囲にあることが,必要十分条件であることは変わりない.
3次関数なので極値の位置で場合分けである.
1.7
[97一橋後期]
問題
1.7
解答
1.7
基本は通る範囲の点であるための必要十分条件を書くことである.
その条件をよく見ると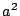 の1次式ではないか.
1次式なら例外を除いて逆に解ける.
の1次式ではないか.
1次式なら例外を除いて逆に解ける.
1.8
[05阪大理系前期]
問題
1.8
解答
1.8
二つの媒介変数があるので,
いずれを固定して考えているのか見極めること.
その点に注意すればよい.
1.9
[05一橋前期]
問題
1.9
解答
1.9
(3)が通過範囲の問題である.どれかの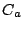 に属するための必要十分条件とは,つまりその点を要素にもつ
に属するための必要十分条件とは,つまりその点を要素にもつ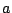 が存在することとして書ける.
統一した考え方のもとに,厳密に論証しよう.
が存在することとして書ける.
統一した考え方のもとに,厳密に論証しよう.
1.10
[07東大]
問題
1.10
解答
1.10
これは逆像法の方が難しくなる場合である.
問題にしたがって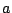 を固定し正像法で
を固定し正像法で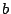 の条件を出すのがよい.
逆像法による解答も研究しよう.
の条件を出すのがよい.
逆像法による解答も研究しよう.
Aozora Gakuen
![]() と
と![]() を
を![]() で表すことである.
そこからとりうる範囲を確定して,
で表すことである.
そこからとりうる範囲を確定して,![]() を消去すればよい.
を消去すればよい.![]() と
と![]() を
を![]() で表すことである.
そこからとりうる範囲を確定して,
で表すことである.
そこからとりうる範囲を確定して,![]() を消去すればよい.
を消去すればよい.![]() を
を![]() を用いて表すと簡単な式になった.
ただし3次式である.しかし
を用いて表すと簡単な式になった.
ただし3次式である.しかし![]() の3次方程式と見て
解が与えられた範囲にあることが,必要十分条件であることは変わりない.
3次関数なので極値の位置で場合分けである.
の3次方程式と見て
解が与えられた範囲にあることが,必要十分条件であることは変わりない.
3次関数なので極値の位置で場合分けである.![]() に属するための必要十分条件とは,つまりその点を要素にもつ
に属するための必要十分条件とは,つまりその点を要素にもつ![]() が存在することとして書ける.
統一した考え方のもとに,厳密に論証しよう.
が存在することとして書ける.
統一した考え方のもとに,厳密に論証しよう.