

 次: 基本定理
上: 積分の方法
前: 積分の方法
次: 基本定理
上: 積分の方法
前: 積分の方法
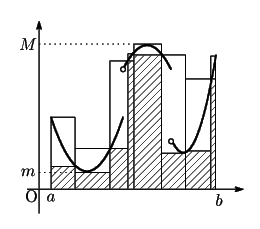
問題を広くとらえるために閉区間で有界な関数 を考える.
関数
を考える.
関数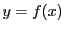 は閉区間
は閉区間 ![$[a,\ b]$](images/img797.gif) で有界であるとし,
この区間における
で有界であるとし,
この区間における の上限を
の上限を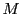 ,下限を
,下限を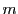 とする.
とする.
区間![$[a,\ b]$](images/img797.gif) を
を 個の小さい有限個の区間に分割する.
個の小さい有限個の区間に分割する. の値の列
の値の列
に対して 個の小区間
個の小区間
をつくる.
小区間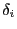 における
における の上限,下限を
の上限,下限を
とする.分割 に対して二つの和を考える.
に対して二つの和を考える.
すると,
 なので,
つまり
なので,
つまり
が成り立つ.
不等式の両端は分割 によらないので,集合
によらないので,集合
はともに有界である.実数の公理によってそれぞれの集合には上限と下限が存在する.
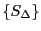 の下限を
の下限を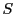 ,
,
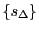 の上限
の上限
ここで二つのことを注意したい.
第一に,関数のグラフで解説したところでわかるように,これはいわば関数と軸で囲まれた領域を有限個の長方形で近似し,そのうえでその上限や下限を考えているということである.はじめから無限個の長方形で近似しているのではない.あらゆる有限個の分割での上限,下限である.
第二に,関数の区間和の図形的意味はグラフで解説されるが,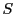 も
も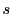 もグラフからは独立に,関数
もグラフからは独立に,関数 に固有の数値として定義されているということである.これらの定義に面積は現れていない.今後の方向を先取りすれば,逆にこの
に固有の数値として定義されているということである.これらの定義に面積は現れていない.今後の方向を先取りすれば,逆にこの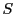 と
と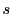 から領域に対してそれが測れるということと,その値としての面積が定義される.
から領域に対してそれが測れるということと,その値としての面積が定義される.
閉区間![$[a,\ b]$](images/img797.gif) の二つの分割
の二つの分割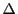 と
と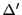 がある.
がある.
このとき
であるなら分割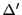 を分割
を分割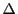 の細分といい,
の細分といい,
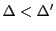 と書く.
と書く.
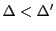 のとき,
のとき,
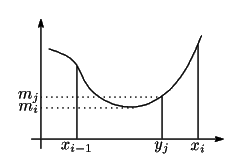
が成り立つ.これを示す.
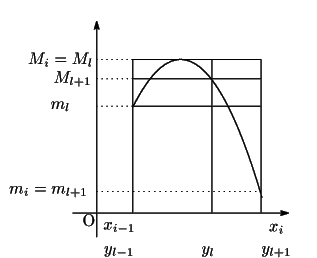
分割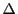 の区間
の区間
![$[x_{i-1},\ x_i]$](images/img1546.gif) が
が
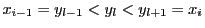 と細分されているとする.
と細分されているとする.
![$
m_i=\inf\{f(x)\ \vert\ x\in [x_{i-1},\ x_i]\}$](images/img1548.gif) ,
,
![$m_l=\inf\{f(x)\ \vert\ x\in [y_{l-1},\ y_l]\}$](images/img1549.gif) ,
,
![$m_{l+1}=\inf\{f(x)\ \vert\ x\in [y_l,\ y_{l+1}]\}$](images/img1550.gif) とすると下限の定義から
とすると下限の定義から
なので
が成り立つ.各区間でこれが成り立つので
である.上限を同様に
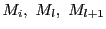 とすると,
とすると,
なので
である.
補題 5
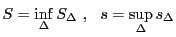
に対し,
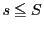
が成り立つ.
■
証明
任意の二つの分割
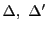 に対して
に対して
である.なぜなら,二つの分割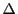 と
と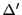 を
を
とするとき,
で作った分割を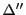 とする.これは
とする.これは
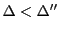 かつ
かつ
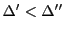 なので
なので
となり,
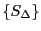 の各要素の値が
の各要素の値が
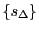 の各要素の値以上となるからである.
□
の各要素の値以上となるからである.
□
分割は無数にある.可算ではない.任意の分割で考えることは実際の計算には不便である.
ところが実は区間の等分割だけを考えればよい.それを保証するのが次の定理である.
分割
に対し,
とおく.
定理 49 (ダルブーの定理)
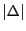
が0に収束する任意の分割列に対し
が成立する.
■
証明
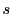 について示す.任意の正の実数
について示す.任意の正の実数 に対して,正の実数
に対して,正の実数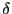 で,
で,
となるものが存在することを示せばよい.
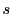 は分割に関する
は分割に関する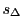 の上限であるから,
の上限であるから,
となる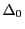 が存在する.
が存在する.
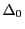 の各小区間の幅の最小値より小さい
の各小区間の幅の最小値より小さい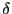 をとる.
そして
をとる.
そして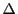 を
を
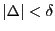 にとる.
すると
にとる.
すると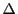 の各小区間には
の各小区間には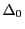 の分点が多くても一つしか含まれない.
二つの分割の分点を合併した分割を分割
の分点が多くても一つしか含まれない.
二つの分割の分点を合併した分割を分割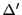 とする.
とする.
 である.
である. 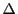 の小区間
の小区間
![$[x_{i-1},\ x_i]$](images/img1546.gif) に
に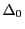 の分点
の分点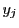 が含まれているときを考える.
つまり
が含まれているときを考える.
つまり
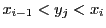 が
が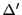 の分割となっているとする.
の分割となっているとする.
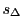 の一項
の一項
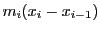 が
が
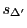 の二項
の二項
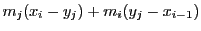 になる.
その差は次のように評価される.
になる.
その差は次のように評価される.
またこのような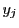 を含まない区間については差は0である.
したがって
を含まない区間については差は0である.
したがって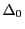 の小区間の個数を
の小区間の個数を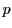 とすると,
とすると,
となる.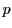 は
は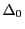 によって固定されているので,
によって固定されているので,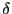 をさらに
をさらに
となるようにとることができる.
よって
となる.これから
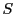 については不等号を逆にとることで同様に示される.
□
については不等号を逆にとることで同様に示される.
□
ダルブーの定理から,次のことがわかる.
関数 が区間
が区間![$[a,\ b]$](images/img797.gif) で有界なとき,
で有界なとき,
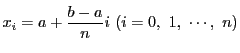 とし,
この
とし,
この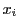 で区間
で区間![$[a,\ b]$](images/img797.gif) を
を 等分する.
区間
等分する.
区間
![$[x_{i-1},\ x_i]$](images/img1546.gif) での関数
での関数 の上限と下限を
の上限と下限を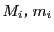 とするとき,
とするとき,
となる.
定義 25
区間
![$[a,\ b]$](images/img797.gif)
で有界な関数

に対し,
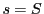
,つまり
が成り立つとき,

は
積分可能(リーマンの意味で)であるという.この一致した値を
と書き,

の

から
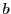
までの
定積分という.
■
上限,下限の定義に従えば, が積分可能であることは「条件:
任意の正数
が積分可能であることは「条件:
任意の正数 に対して,分割
に対して,分割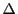 で
で
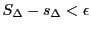 となるものが存在する」が成立することと同値である.
そして,
となるものが存在する」が成立することと同値である.
そして,
 のことを被積分関数という.
また,定積分で
のことを被積分関数という.
また,定積分で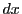 のところの
のところの を積分変数という.
を積分変数という.
注意 5.1
積分変数は定積分の中だけで使われる変数で,
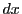
の

と

の

が同じ文字であれば,どのような文字を使ってもかまわない.ただし,被積分関数が
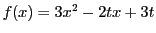
のように文字を含むときは,
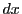
や
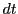
で,どの文字の関数として積分するのかを指示している.
定積分を後のルベーグ積分と区別するときにはリーマン積分ともいう.
リーマンがはじめて積分を関数固有のものとして定義した.
リーマン(Georg Friedrich Bernhard Riemann,1826〜1866)は19世紀ドイツの数学者,現代にいたるまで何度も何度もその偉大さが再認識されていくという偉人である.
定理 50
区間
![$[a,\ b]$](images/img797.gif)
で有界な関数

が積分可能とする.
区間の分割
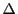
の各小区間
![$\delta_i=[x_{i-1},\ x_i]\ (i=1,\ 2,\ \cdots,\ n)$](images/img1596.gif)
の内の任意の点
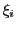
をとる.このとき
が成立する.
■
証明
それぞれの区間での関数値の上限と下限をこれまでと同様に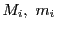 とする.
各
とする.
各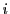 に対して,
に対して,
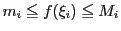 であるから,
であるから,
 が積分可能なので,
が積分可能なので,
したがって,任意の正数 に対して,
正数
に対して,
正数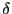 で
で
となるものが存在する.
□
本定理の右辺の和
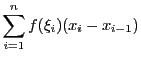 を
定積分
を
定積分
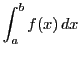 に対するリーマン和という.
に対するリーマン和という.
系 50.1
区間
![$[a,\ b]$](images/img797.gif)
で有界な関数

が積分可能とする.
区間を

等分し
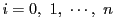
に対して
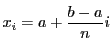
とする.またこの分割を
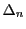
とする.このとき,
証明
前半の等号は定理49から,
後半の等号は定理50から成立する.
□
注意 5.2
2008年の高校微積教科書で,等式
は,
区分求積法といわれる.
この等式の両辺とも,面積は関係なく定まる.
にもかかわらず,これを区分求積法という.
その結果,高校生は,
まず関数のグラフと座標軸で囲まれた領域に面積というものがあり,
それが左辺の数列の和の極限として表され,
それを右辺の定積分で計算する公式,として理解する.
系50.1によって,連続関数ではこの等式が成立することがわかる.
しかし,本来この等式の意味は,
系50.1によって,連続関数の場合,これが定積分の定義式そのものである,
ということである.
面積を大前提とするかぎり,測度を理解することはできない.
これが日本の高校数学の事実である.
定理 51
閉区間
![$[a,\ b]$](images/img797.gif)
で単調な関数

は積分可能である.
■
証明
関数 が単調増加であるとする.
区間
が単調増加であるとする.
区間![$[a,\ b]$](images/img797.gif) の分割
の分割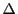 の小区間を
の小区間を
![$\delta_i=[x_{i-1},\ x_i]\quad (i=1,\ 2,\ \cdots,\ n)$](images/img1612.gif) とする.
とする.
 が単調なので
が単調なので
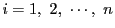 に対して
に対して
である.したがって
となる.
任意の正数 が与えられたとき分割
が与えられたとき分割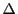 を
を
となるようにとる.このとき
よって,単調増加関数は積分可能である.
同様に単調減少関数も積分可能である.
□
例 5.1
区間
![$[0,\ 1]$](images/img1498.gif)
内の

を
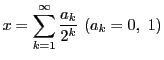
と二進展開する.関数

を
で定める.

は単調増加関数である.
だが連続ではない.
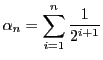
とすると
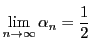
であるが,
なので

は
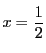
で連続ではない.
一般に

は,奇素数
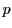
に対する
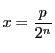
で連続ではない.
しかし積分可能である.区間![$[0,\ 1]$](images/img1498.gif) を
を
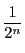 等分し,分点を
等分し,分点を
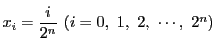 とする.
とする.
であるが.
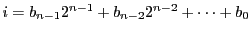
とする.
ただし
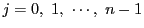
に対し,
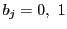
のいずれかの値である.このとき
なので,
ただし,和は
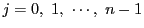
に対し
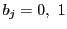
のすべての場合にわたる.各
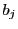
は
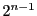
回ずつ現れるので,
よって
このように単調であれば不連続点が稠密に入っていても積分可能なことがある.
例 5.2

を区間
![$[0,\ 1]$](images/img1498.gif)
において

が有理数なら
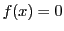
,

が無理数なら
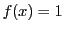
で定義する.

は有界である.
しかしどのように小区間を構成しても,有理数が稠密にあるので
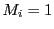
,
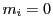
となる.
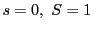
でこれが一致することはない.
積分可能ではない.
定理 52
閉区間
![$[a,\ b]$](images/img797.gif)
で連続な関数

は積分可能である.
■
証明
 は有界閉区間で連続であるから,一様連続である.
任意の正数
は有界閉区間で連続であるから,一様連続である.
任意の正数 に対して正数
に対して正数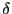 で
で
となるものが存在する.
分割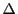 を
を
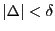 となるようにとる.
となるようにとる.
 は連続なので
は連続なので
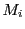 と
と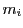 は小区間
は小区間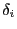 における最大値と最小値である.
における最大値と最小値である.
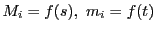 とすると
とすると
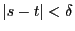 なので
なので
である.よって
よって,連続関数は積分可能である.
□
注意 5.3
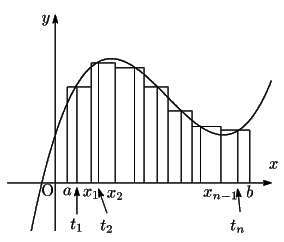
1969年の日本書院の教科書の数学IIIで,
定積分は次のように定義されている.
関数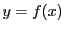 は閉区間
は閉区間 ![$[a,\ b]$](images/img797.gif) で連続とする.
この区間を図のように
で連続とする.
この区間を図のように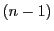 個の点
個の点
で

個の小区間
に分ける.それら小区間内にそれぞれ任意の点
をとって,和
を作る.
すべての小区間の長さが,いずれも0に近づくように

を限りなく大きくするとき,
の点のとり方にかかわらず,
和
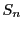
は一定の極限値に近づくことが知られている.
この極限値を,関数

の区間
![$[a,\ b]$](images/img797.gif)
における
定積分といい
で表す.
■
この定義は高校生のための定積分の定義として優れている.
リーマン積分の理論と断絶することなく,そこに開かれている.
「収束」の意味,区間和の上限,下限などを学習し,
連続関数なら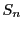 が収束すること,積分可能であることをつかんだ段階で,
高校での定義を再認識することができる.
高校教科書はこのようでなければならない.
が収束すること,積分可能であることをつかんだ段階で,
高校での定義を再認識することができる.
高校教科書はこのようでなければならない.


 次: 基本定理
上: 積分の方法
前: 積分の方法
次: 基本定理
上: 積分の方法
前: 積分の方法
2014-05-23
![]() を
を![]() 個の小さい有限個の区間に分割する.
個の小さい有限個の区間に分割する.![]() の値の列
の値の列
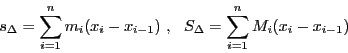

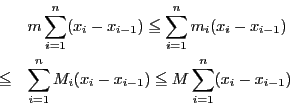
![]() も
も![]() もグラフからは独立に,関数
もグラフからは独立に,関数![]() に固有の数値として定義されているということである.これらの定義に面積は現れていない.今後の方向を先取りすれば,逆にこの
に固有の数値として定義されているということである.これらの定義に面積は現れていない.今後の方向を先取りすれば,逆にこの![]() と
と![]() から領域に対してそれが測れるということと,その値としての面積が定義される.
から領域に対してそれが測れるということと,その値としての面積が定義される.
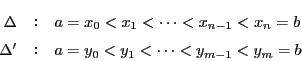

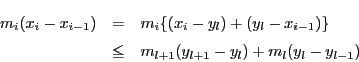
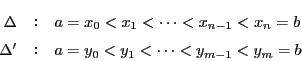
![]() は分割に関する
は分割に関する![]() の上限であるから,
の上限であるから,
 である.
である. 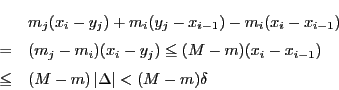
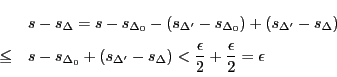
![]() については不等号を逆にとることで同様に示される.
□
については不等号を逆にとることで同様に示される.
□
![]() が区間
が区間![]() で有界なとき,
で有界なとき,
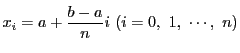 とし,
この
とし,
この![]() で区間
で区間![]() を
を![]() 等分する.
区間
等分する.
区間
![]() での関数
での関数![]() の上限と下限を
の上限と下限を![]() とするとき,
とするとき,
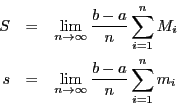
![]() が積分可能であることは「条件:
任意の正数
が積分可能であることは「条件:
任意の正数![]() に対して,分割
に対して,分割![]() で
で
![]() となるものが存在する」が成立することと同値である.
そして,
となるものが存在する」が成立することと同値である.
そして,
![]() のことを被積分関数という.
また,定積分で
のことを被積分関数という.
また,定積分で![]() のところの
のところの![]() を積分変数という.
を積分変数という.
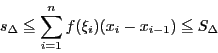
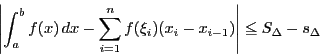
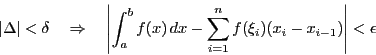
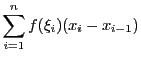 を
定積分
を
定積分
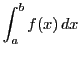 に対するリーマン和という.
に対するリーマン和という.
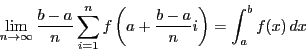
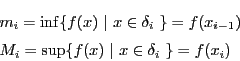
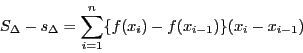
![]() が与えられたとき分割
が与えられたとき分割![]() を
を
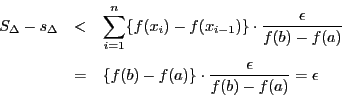
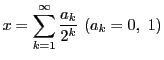 と二進展開する.関数
と二進展開する.関数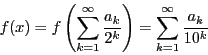
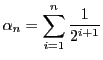 とすると
とすると
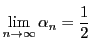 であるが,
であるが,
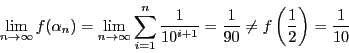
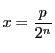 で連続ではない.
で連続ではない.
![]() を
を
![]() 等分し,分点を
等分し,分点を
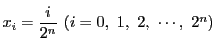 とする.
とする.
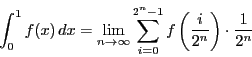
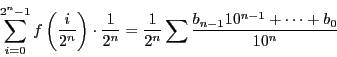
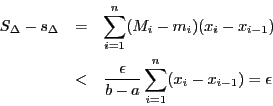
![]() は閉区間
は閉区間 ![]() で連続とする.
この区間を図のように
で連続とする.
この区間を図のように![]() 個の点
個の点
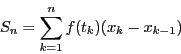
![]() が収束すること,積分可能であることをつかんだ段階で,
高校での定義を再認識することができる.
高校教科書はこのようでなければならない.
が収束すること,積分可能であることをつかんだ段階で,
高校での定義を再認識することができる.
高校教科書はこのようでなければならない.