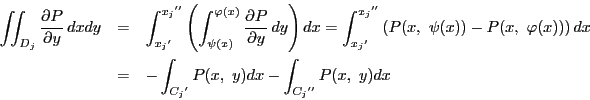次: 微分方程式
上: 次元の拡大
前: 微分と幾何
次: 微分方程式
上: 次元の拡大
前: 微分と幾何
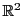 内の有界領域
内の有界領域 で定義された実数値をとる有界関数
で定義された実数値をとる有界関数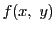 がある.
がある.
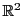 内の長方形
内の長方形
![$R=[a,\ b]\times [\alpha,\ \beta]$](images/img2362.gif) で
で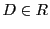 となるものを取る.
区間
となるものを取る.
区間![$[a,\ b]$](images/img797.gif) ,
,
![$[\alpha,\ \beta]$](images/img1711.gif) をそれぞれ分割し,
をそれぞれ分割し,
とする.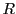 を小長方形
を小長方形
![$\omega_{ij}=[x_{i-1},\ x_i]\times[y_{j-1},\ y_j]$](images/img2365.gif) に分割する.関数
に分割する.関数 を
を
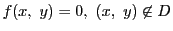 とすることで
とすることで
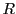 で定義された関数に拡張する.
で定義された関数に拡張する.
そして
とし,
とする.分割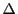 の細分
の細分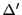 に対して
に対して
となる.そして
とする.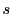 や
や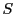 が存在する場合は,
が存在する場合は,
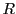 を含むより大きな長方形
を含むより大きな長方形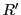 を取っても
を取っても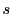 と
と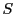 の値は不変である.
よって
の値は不変である.
よって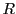 のとり方にはよらない.
のとり方にはよらない.
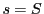 が成り立つとき,
が成り立つとき,
 は
は において積分可能といい,この値を
において積分可能といい,この値を
のように書く.
これが基本的な重積分の定義であり,
一変数のときのリーマン積分と同じ思想圏内の定義である.
定理 77
関数

が

で連続で

が可測なら,

は

で積分可能である.
■
証明
 は有界であるから
は有界であるから は
は で一様連続である.
で一様連続である.
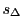 と
と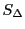 を定義する和
を定義する和
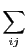 を
を
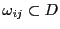 となるものにわたる和
となるものにわたる和
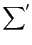 と,
と,
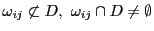 にわたる和
にわたる和
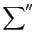 に分ける.
に分ける. と交わらない
と交わらない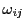 においては
においては
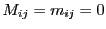 である.
である.
正の数 が与えられたとする.
正の数
が与えられたとする.
正の数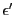 を仮にとる.
を仮にとる.
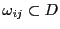 に対しては,
に対しては, の一様連続性から
細分化された分割
の一様連続性から
細分化された分割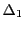 で
で
となるものが存在する.従って
また
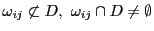 においては
においては
 が可測であることから細分化された分割
が可測であることから細分化された分割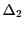 で
で
となるものがある. において
において は有界なので
は有界なので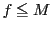 となる定数がある.
従って
となる定数がある.
従って
2つの分割からなる細分された分割を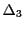 とする.
この分割に対しては
とする.
この分割に対しては
が成立する.従って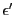 を
を
となるようにとれば,与えられた正の数 に対して
に対して
となる分割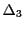 が存在することが示された.
つまり
が存在することが示された.
つまり
となり, が積分可能であることが示された.
□
領域
が積分可能であることが示された.
□
領域 で定義された関数
で定義された関数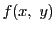 が積分可能なとき,積分値
が積分可能なとき,積分値
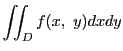 を
を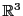 の部分集合
の部分集合
の体積という.
二次元の場合のように三次元空間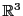 の部分集合の可測性について論じることもできる.
重積分の計算は,一変数の積分のくりかえし(累次積分)で計算する.
の部分集合の可測性について論じることもできる.
重積分の計算は,一変数の積分のくりかえし(累次積分)で計算する.
 は領域
は領域 で定義されているものとするが,
で定義されているものとするが, が可測なときは
が可測なときは の外で
の外で の値を0とすることで
の値を0とすることで
 を長方形に拡張した.
を長方形に拡張した. が
が で積分可能なら,
で積分可能なら, はこの長方形で定義された関数として長方形で積分可能である.従って長方形で積分可能な関数が与えられているとする.
はこの長方形で定義された関数として長方形で積分可能である.従って長方形で積分可能な関数が与えられているとする.
定理 78
関数
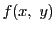
が長方形
![$R=[a,\ b]\times [\alpha,\ \beta]$](images/img2362.gif)
で有界で積分可能とする.
![$x\in [a,\ b]$](images/img2394.gif)
を固定するたびに,
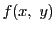
が

について

から
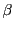
まで積分可能であるとする.このとき
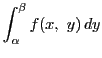
は

の関数として

から
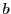
まで積分可能で,
が成り立つ.
■
証明
記号はこれまでと同じものとする.
![$\xi_i\in [x_{i-1},\ x_i]$](images/img2397.gif) に対して
に対して
である.従って
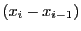 をかけて
をかけて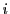 について加えると
について加えると
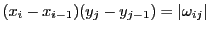 なので
なので
 が
が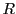 で積分可能なので
で積分可能なので
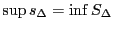 である.
よってははさみうちの原理から
である.
よってははさみうちの原理から
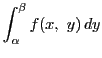 は
は の関数として積分可能で,
の関数として積分可能で,
が成り立つ.
□
以上は二変数の場合について論じたが,同様にして任意の次元の重積分と累次積分の関係に拡張される.
また一変数の場合の置換積分の理論に対応する,
変数変換
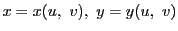 と積分の理論も重要である.
ここでは証明は行わないが次の定理が成り立つ.証明は『解析概論』§96「変数の変換」を見てほしい.
と積分の理論も重要である.
ここでは証明は行わないが次の定理が成り立つ.証明は『解析概論』§96「変数の変換」を見てほしい.
定理 79
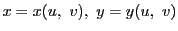
が
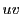
平面上の領域

と
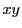
平面上の領域
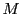
の間の一対一対応を与え,
関数
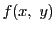
が
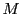
で積分可能であるならば
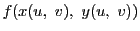
は

で積分可能であり
となる.
■
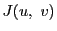 のことを関数行列式またはヤコビアンという.
また変数を明示して
のことを関数行列式またはヤコビアンという.
また変数を明示して
と表すことも多い.すぐに確認できるが
であるとき.
が成り立つ.
例 6.8
極座標変換.
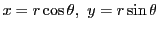
とすると,
つまり
この応用として等式
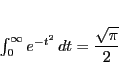 |
(2) |
を示そう.
関数
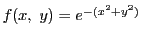 と領域
と領域
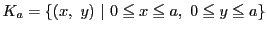 をとり,この領域での
をとり,この領域での の重積分を
の重積分を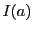 とする.
とする.
次に同じ

の領域
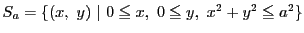
での重積分を
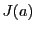
とする.これを極座標で計算する.
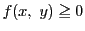
で
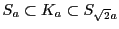
であるから
ところが
なのではさみうちの原理から
となり等式(
2)が得られた.
平面上の領域 上で定義された連続関数
上で定義された連続関数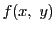 と
と
 内の曲線
内の曲線
がある.曲線を分割し
とする.ただし,
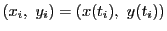 となる
となる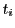 が
が
となるようにとられているものとする.曲線 の
点
の
点
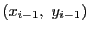 と点
と点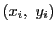 で切られる部分上の
で切られる部分上の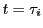 に対応する点
に対応する点
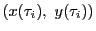 をとり,
和
をとり,
和
をとる.
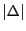 は分割された隣りあう二点間の距離の最大値とする.
は分割された隣りあう二点間の距離の最大値とする.
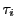 をどのように選んでも,極限
をどのように選んでも,極限
が存在し一定であるとき,その極限値を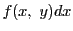 の
の に沿う線積分といい
に沿う線積分といい
と表す.同様に
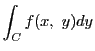 も定義される.
特に
も定義される.
特に が閉曲線のとき一周して積分することを示すために
が閉曲線のとき一周して積分することを示すために
と表すことも多い.
曲線 が,
有限個の点を除いて滑らかであるとき,
つまり
が,
有限個の点を除いて滑らかであるとき,
つまり 成分と
成分と 成分がともに有限個の点を除いて微分可能であるとき,
これを区分的に滑らかということにする.
成分がともに有限個の点を除いて微分可能であるとき,
これを区分的に滑らかということにする.
定理 80
曲線

が区分的に滑らかなら

に沿う線積分が存在し,
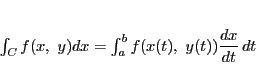 |
(3) |
で与えられる.
■
証明
曲線 に微分不能な点があるとき,
それらの点で曲線を滑らかな部分に分割し,
その各々の部分で等式(3)が成立することが示されれば,
その後それらの両辺を加えればよい.
従って
に微分不能な点があるとき,
それらの点で曲線を滑らかな部分に分割し,
その各々の部分で等式(3)が成立することが示されれば,
その後それらの両辺を加えればよい.
従って は滑らかであるとして示せばよい.
は滑らかであるとして示せばよい.
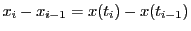 に平均値の定理を用いると,
に平均値の定理を用いると,
となる
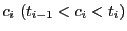 がとれ
がとれ
となる.
一方,線積分が存在するので
となる.よって等式(3)が示された.
□
注意 6.5
線積分は

の分割で定義されている.
従って媒介変数
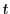
のとり方によらない.
曲線 が単一閉曲線であるとは,
が単一閉曲線であるとは,
とするとき,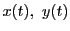 は連続で
は連続で
が成り立つことであった.
また,平面上の領域が弧状連結であるとは,
その領域内の任意の二点に対して,
その二点を結び領域内を通る連続曲線が存在することとする.
次の定理が成り立つ.
定理 81 (ジョルダンの曲線定理)
平面上の単一閉曲線

は,平面を二つの弧状連結な部分に分割される.
その一方は有界であり,
他方は有界でない.一方の部分の点と他方の部分の点を結ぶ連続曲線は,

と共有点をもつ.
■
この厳密な証明は簡単ではない.
平面上の単一閉曲線 で分けられる二つの部分のうち
有界な部分を内部といい,内部が左になるように進む曲線上の方向を正の向き,反対方向を負の向きという.
で分けられる二つの部分のうち
有界な部分を内部といい,内部が左になるように進む曲線上の方向を正の向き,反対方向を負の向きという.
定理 82
曲線

は
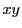
平面上の区分的に滑らかな単一閉曲線であるとする.

上正の方向に動くとき,

方向の増加と減少が変化する点が有限個であり,

方向の増減についても同様であるとする.
このとき曲線内部の面積
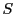
は
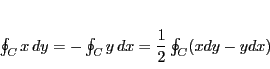 |
(4) |
で与えられる.ただし,線積分は

の正の方向にとるものとする.
■
証明
![$C:\mathrm{P}(t)=(x(t),\ y=y(t)),\ t \in [a,\ b]$](images/img2454.gif) とし,
とし,
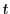 が増加するとき点
が増加するとき点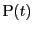 は曲線上を正の向きに動くものとする.
は曲線上を正の向きに動くものとする.
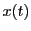 の増減が変化する
の増減が変化する の値で
の値で 軸平行な直線を引き曲線と曲線内部を分割する.
図のように
二点
軸平行な直線を引き曲線と曲線内部を分割する.
図のように
二点
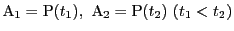 ではさまれた曲線
ではさまれた曲線 の部分を
の部分を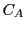 とし,
同じ
とし,
同じ の値で定まる
二点
の値で定まる
二点
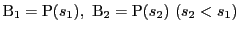 ではさまれた曲線
ではさまれた曲線 の部分を
の部分を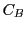 とする.
とする.
 このとき
このとき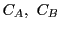 および二直線で囲まれた領域の面積は
および二直線で囲まれた領域の面積は
このような部分面積の総和が面積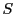 なので
これらを加えることにより
なので
これらを加えることにより
を得る. 方向の積分で考えるときは,
方向の積分で考えるときは,
 の増加の方向と
の増加の方向と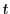 の増加の方向が
の増加の方向が
 軸で考えるときの逆になるので
軸で考えるときの逆になるので
となる.この二つを加えることにより等式4
が得られる.
□
曲線内部の面積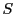 を
を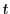 の積分で表せば
の積分で表せば
となる.
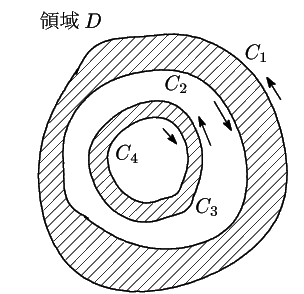 有限個の互いに共有点をもたない単一閉曲線が偶数個あり, 順にそれが定める領域の内部にあるとする. それを
有限個の互いに共有点をもたない単一閉曲線が偶数個あり, 順にそれが定める領域の内部にあるとする. それを
 とする.奇数番を左回り,偶数番を右回りにとると,
とする.奇数番を左回り,偶数番を右回りにとると,
 と
と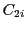 の進む方向の左側にある部分(曲線自身は含まない)として領域が定まり,
それらの和で領域
の進む方向の左側にある部分(曲線自身は含まない)として領域が定まり,
それらの和で領域 が定まる.
このような領域が互いに交わることなく有限個ある場合も同様に考えることができる.
が定まる.
このような領域が互いに交わることなく有限個ある場合も同様に考えることができる.
このとき,有界な領域 は,有限個の単一閉曲線群によって定まっているという.
そして,これらの方向付けらられた曲線の群を領域
は,有限個の単一閉曲線群によって定まっているという.
そして,これらの方向付けらられた曲線の群を領域 の境界といい
の境界といい
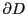 と表す.境界は
と表す.境界は の閉包
の閉包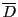 から
から 自身を除いた集合に,
向きをつけたものに他ならない.
自身を除いた集合に,
向きをつけたものに他ならない.
以上の準備のもとに定理82の拡張である,平面の場合のグリーンの定理を示す.
本来のグリーンの定理は空間におけるベクトル解析の重要な定理である.
定理 83 (グリーンの定理)
有界な領域

が,
有限個の区分的に滑らかな単一閉曲線群によって(先に述べたように)定まっているとする.
この曲線群を定める各曲線において

方向の増加と減少が変化する点が有限個であるとする.
二つの関数

が領域

で偏微分可能で,
それら導関数が閉領域
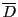
で連続であるとする.
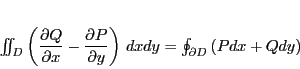 |
(5) |
が成り立つ.
■
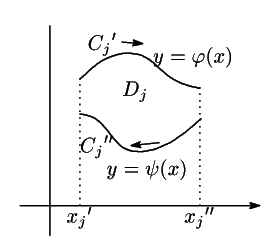 証明
証明
 方向の増減が変化する
方向の増減が変化する の値,および
の値,および 成分の微分係数が存在しない
成分の微分係数が存在しない の値で
の値で
 軸平行な直線を引き,
領域
軸平行な直線を引き,
領域 とその境界
とその境界 を分割する.
その一つ
を分割する.
その一つ と
と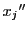 で区切られた部分を
で区切られた部分を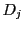 とし,分割された境界
とし,分割された境界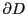 の部分を
の部分を
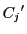 と
と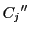 とする.
曲線
とする.
曲線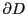 の媒介変数表示を
の媒介変数表示を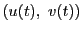 とすると,
とすると,
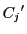 の部分では
の部分では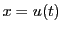 は一対一であり逆関数を持つ.
それを
は一対一であり逆関数を持つ.
それを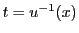 とすると
とすると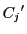 は
は
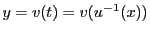 と
と と
と の関数で表される.
これを
の関数で表される.
これを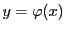 と表すことができる.
と表すことができる.
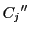 についても同様である.これを
についても同様である.これを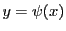 とする.
このとき
とする.
このとき
これらをすべて加えると重積分の積分領域は となり,
線積分の積分域は境界
となり,
線積分の積分域は境界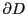 となる.よって
となる.よって
同様に 軸平行な直線で分けることにより,
軸平行な直線で分けることにより,
が示され等式5が得られる.
□
注意 6.6
定理
82は本定理において
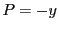
,
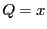
としたものである.
グリーンという人はどのような人だったのか.
『数学セミナー』2003年7月号
に「知られざるグリーン」(岡本久著)がある.
その伝記部分を引用させてもらい紹介したい.
グリーンの公式を見い出したジョージ・グリーンは大変興味深い人物である.
1793年に生まれ,1841年に病没しているが,詳しいことは分かつていない.
彼がグリーンの公式を含む論文(エッセイと名付けられている)を発表したのはイギリス中部のノッチンガム
(Nottingham)という工業都市であった.その論文ではグリーンの公式ももちろん導かれているが,
もっと重要なのはいわゆるグリーン関数というものを定義したことである.
この考え方はきわめて革新的なものであった.
彼の論文は著名な専門雑誌に戴ったわけではなく,自費出版に近いものであったようである.
ノッチンガムはロビン・フッドの冒険で有名な都市であるが,
学問の中心であるケンブリッジとかオックスフォードとはあまり縁のなさそうな場所である.
そのようなところでどうして革新的なアイデアが生まれたのであろうか?
グリーンの父親は地元で繁盛したパン屋さんで,事業を拡大して粉屋も開業し,
産業革命の発展による賃金労働者(その人々は当然パンを自分で作るのではなくお金で買うことになる)
の爆発的な増加のおかげて相当な資産家になったという.
家業を継いだグリーンは高等教育は受けていなかったのだが,
独学でフランスの論文(ケンブリッジやオックスフォードではないことに注意されたい)を読んで,
自分流の考えを発展させたらしい.「らしい」というのはよくわかっていないからで,
彼の偉大な論文も20年ほどはまったく忘れ去られ,
死後にウィリアム・トムソン(William Thomson)によってそのアイデアの革新性が認識されるまでまわりに理解されなかったのである.
彼の遺族もグリーンがそのような偉大な人物であるとは思わず,
さまざまな資料が散逸してしまったようである.
もちろん肖像画などが残ることもなかった.
さて,彼は粉屋の仕事を続けながら独学をしていたが,
若い頃は父親の学問に対する無理解もあって学問に専念できなかった.
父の死後,家業を番頭格の人物に預けて学問に本格的に進み,
35歳で最初の,そして歴史に残る偉大な論文をたった一人で書き上げたのである.
独学の天才はグリーン以外にもいる.電磁誘導の発見などで有名なファラデーもほぼ同時代の人物で,
大学を出たわけではないが,実験物理学で不朽の業績をあげている.
しかし,ファラデーの場合は王立研究所の助手として出発し,
優れた研究環境が彼のまわりに存在していた.
これに対し,グリーンはアドバイスをしてくれる人物もなく完全な独学であった点は多い
に強調されるべきであろう.このような仕事が一地方都市で,
しかも数学者としては異例の晩生人間によって,
独学で達成されたのは当時のイギリスという国の底力を表しているようにも思える.
(もちろん江戸時代の我が国にも上流階級出身でないのに和算で名をなした人物もいるけれど…)
残念なことにあまりに革新的な考え方はすぐには認められず,
長生きしなかったせいもあって,長い間彼に栄誉が与えられることはなかった.
しかし,グリーンのアイデアは現在の数理物理学には不可欠のものとなっており,
その名誉を讃え,
現在ではウエストミンスター寺院のアイザック・ニュートンの近くに葬られているという.
実に感慨深い話しではないか.


 次: 微分方程式
上: 次元の拡大
前: 微分と幾何
次: 微分方程式
上: 次元の拡大
前: 微分と幾何
2014-05-23
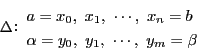
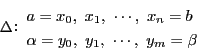
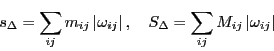
![]() が成り立つとき,
が成り立つとき,
![]() は
は![]() において積分可能といい,この値を
において積分可能といい,この値を
![]() が与えられたとする.
正の数
が与えられたとする.
正の数![]() を仮にとる.
を仮にとる.
![]() に対しては,
に対しては,![]() の一様連続性から
細分化された分割
の一様連続性から
細分化された分割![]() で
で
![]() においては
においては
![]() が可測であることから細分化された分割
が可測であることから細分化された分割![]() で
で
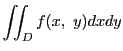 を
を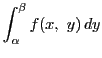 は
は
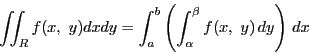
![]() に対して
に対して
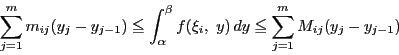
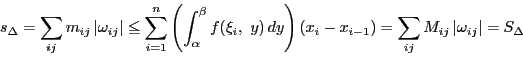
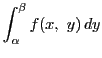 は
は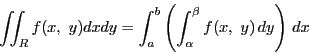
![]() と積分の理論も重要である.
ここでは証明は行わないが次の定理が成り立つ.証明は『解析概論』§96「変数の変換」を見てほしい.
と積分の理論も重要である.
ここでは証明は行わないが次の定理が成り立つ.証明は『解析概論』§96「変数の変換」を見てほしい.
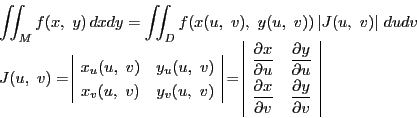
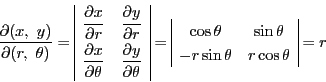
![]() と領域
と領域
![]() をとり,この領域での
をとり,この領域での![]() の重積分を
の重積分を![]() とする.
とする.
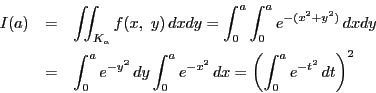
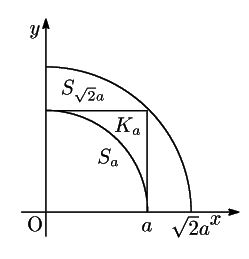
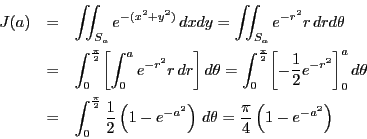
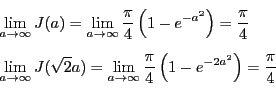
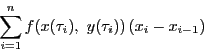
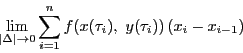
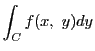 も定義される.
特に
も定義される.
特に![]() が,
有限個の点を除いて滑らかであるとき,
つまり
が,
有限個の点を除いて滑らかであるとき,
つまり![]() 成分と
成分と![]() 成分がともに有限個の点を除いて微分可能であるとき,
これを区分的に滑らかということにする.
成分がともに有限個の点を除いて微分可能であるとき,
これを区分的に滑らかということにする.
![]() に平均値の定理を用いると,
に平均値の定理を用いると,
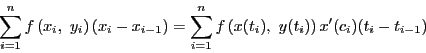
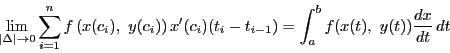
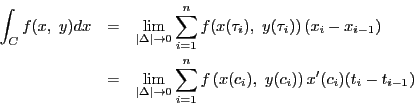
![]() が単一閉曲線であるとは,
が単一閉曲線であるとは,
![]() で分けられる二つの部分のうち
有界な部分を内部といい,内部が左になるように進む曲線上の方向を正の向き,反対方向を負の向きという.
で分けられる二つの部分のうち
有界な部分を内部といい,内部が左になるように進む曲線上の方向を正の向き,反対方向を負の向きという.
 このとき
このとき![]() および二直線で囲まれた領域の面積は
および二直線で囲まれた領域の面積は
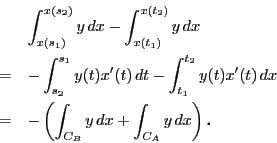
![]() を
を![]() の積分で表せば
の積分で表せば
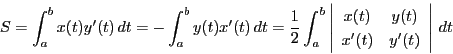
 有限個の互いに共有点をもたない単一閉曲線が偶数個あり, 順にそれが定める領域の内部にあるとする. それを
有限個の互いに共有点をもたない単一閉曲線が偶数個あり, 順にそれが定める領域の内部にあるとする. それを
![]() は,有限個の単一閉曲線群によって定まっているという.
そして,これらの方向付けらられた曲線の群を領域
は,有限個の単一閉曲線群によって定まっているという.
そして,これらの方向付けらられた曲線の群を領域![]() の境界といい
の境界といい
![]() と表す.境界は
と表す.境界は![]() の閉包
の閉包![]() から
から![]() 自身を除いた集合に,
向きをつけたものに他ならない.
自身を除いた集合に,
向きをつけたものに他ならない.
 証明
証明