

 次: 整数の公理
上: 集合と公理
前: 対応と写像
次: 整数の公理
上: 集合と公理
前: 対応と写像
以上述べた集合の定義はカントールの時代のものである.それからまもなくこの定義ではいろいろな矛盾が生まれることが知られていった.次のラッセル(Bartland Russell 1872〜1970)の逆理がそのもっとも重要なものである.
 を,それ自身を要素に含まない集合
を,それ自身を要素に含まない集合 の集合とする.つまり
の集合とする.つまり
このとき,
となり矛盾である.
このような矛盾が「数学の危機」といわれる反省をもたらし,数学基礎論を発展させた.集合論についていえば公理的集合論を生み出すのである.それに対してこれまで述べた集合の定義にもとづく集合論は素朴集合論といわれる.
このような矛盾を退けるような公理体系が,いくつか提出された.そのはじめは1908年のツェルメロであった.それを補強したのがフランケルでこれをツェルメロ−フランケルの集合論という.それは次のような公理系よりなる.論理記号で書くと次のようになる.これらは,集合を表す文字と関係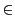 ,および全称全称記号「∀」と存在記号「∃」,そしてその否定「¬」,そして仮定と結論を結ぶ「⇒」とかかり方を表す括弧「( )」のみで書かれる.
,および全称全称記号「∀」と存在記号「∃」,そしてその否定「¬」,そして仮定と結論を結ぶ「⇒」とかかり方を表す括弧「( )」のみで書かれる.
ツェルメロ−フランケルの公理系はZF公理系と言われる.
このように,公理的集合論によって数学の言葉としての集合は,これまで通り用いることができる.もとより公理系そのものが改訂されてゆく.上記公理系も,ツェルメロ−フランケルのものからさらに,フォンノイマンによって拡張されたものである.また,これとは別に,ベルナイスーゲーデルの公理系がある.二つの公理系は一方から他方が導かれ同等であることが知られている.
次の公理を選択公理という.
- 10.
- 選択公理:
ここで は
は で定義された関数である.
このような関数はグラフによって決定される.
で定義された関数である.
このような関数はグラフによって決定される.
 は,
は,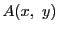 によって定まる集合の要素である.
によって定まる集合の要素である.
この論理式の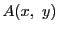 が
が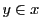 のときの意味は,
のときの意味は, に属する集合が空でないとき,各
に属する集合が空でないとき,各 から
から の要素を選ぶ関数が存在するということである.それを論理式に書くと次のようになる.
の要素を選ぶ関数が存在するということである.それを論理式に書くと次のようになる.
 が互いに交わらない空でない集合の集合のとき,
が互いに交わらない空でない集合の集合のとき, の要素である集合から要素を選んだ集合
の要素である集合から要素を選んだ集合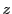 が存在する.ZF公理系のなかでは,この形の公理は上記選択公理と同値になる.
が存在する.ZF公理系のなかでは,この形の公理は上記選択公理と同値になる.
選択公理は,素朴集合論の言葉では次のような命題となる.ここでは集合を大文字で書く.
- 集合
 の部分集合の族
の部分集合の族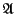 において,
において,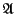 が空集合を含まないとき,
が空集合を含まないとき,
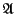 に属する各部分集合
に属する各部分集合 に
に に属する要素
に属する要素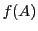 を一意に対応させる関数
を一意に対応させる関数 が存在する.
が存在する.
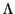 を添え字の集合とする集合の族
を添え字の集合とする集合の族
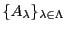 において,
において,
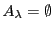 となる
となる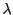 が存在しないなら,
その直積集合
が存在しないなら,
その直積集合
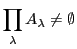 である.
である.
- 集合
 が,
が,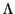 を添え字の集合とする部分集合の族
を添え字の集合とする部分集合の族
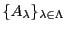 の直和
の直和
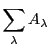 であるとき,
各
であるとき,
各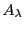 とただ一つの要素を共有する
とただ一つの要素を共有する の部分集合が存在する.
の部分集合が存在する.
- 集合
 から集合
から集合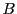 への全射
への全射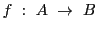 に対して,写像
に対して,写像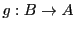 で,
で,
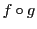 が
が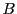 から
から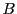 への恒等写像となるものが存在する.
への恒等写像となるものが存在する.
ZF公理系に選択公理を加えた公理系をZFC公理系と言う.集合の公理系に選択公理を加えた公理系が素朴集合論と合致する集合である.
選択公理はごく自然な公理であり,論述の中で意識せずに用いられることも繰り返されてきた.集合論の基礎を再確認しようとするなかで,これが自明なことではなく,用いる以上は公理としてあげねばならないことであることが認識されたのは,20世紀の初頭であった.
しかしこの自然な公理の定式化が,集合論におけるもっとも深い事実をつぎつぎに明らかにした.
集合の公理系を考えることは,素朴集合論で現れる矛盾を回避するためどのように集合の公理系をつくればよいのか,という問題にはじまった.しかしこのように用いる論理を明確にし,集合の公理を立て厳格な論証をおこなうことによって,集合論の深い定理が見出された.それが選択公理とツォルンの補題そして整列可能定理の同値性である.
ここでは,その証明はおこなわない.選択公理や整列可能定理に含まれる概念の定義と,得られる結論のみをのべる.
いくつかの定義.
定義 4
- 集合
 は要素の間の関係
は要素の間の関係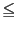 が
が
を満たすとき,この関係を順序という.
順序をもつ集合 を半順序集合という.
関係を明記するときは
を半順序集合という.
関係を明記するときは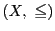 と記す.■
と記す.■
- 半順序集合
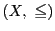 の任意の2つの要素
の任意の2つの要素 と
と に対し
に対し
のいずれかが定まるとき,集合 は全順序集合であるという.■
は全順序集合であるという.■
半順序集合または全順序集合を順序集合という.
順序集合においてさらに次の概念を定義する.
定義 5
- 半順序集合
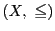 の空でない部分集合
の空でない部分集合 に対し,
に対し,
が成り立つ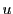 を
を の一つの上界という.■
の一つの上界という.■
- 半順序集合は,その任意の全順序部分集合が上界をもつとき,
帰納的であるという.■
- 半順序集合
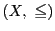 の要素
の要素 は,
は,
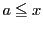 かつ
かつ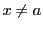 である要素
である要素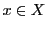 が存在しないとき,
極大要素であるという.■
が存在しないとき,
極大要素であるという.■
- 半順序集合
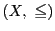 の空でない部分集合
の空でない部分集合 に対し,
に対し,
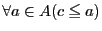 となる
となる の要素
の要素 を,
を,
 の最小要素という.■
の最小要素という.■
- 半順序集合
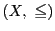 は,
その空でない部分集合
は,
その空でない部分集合 がつねに最小要素をもつとき,
整列集合であるという.■
がつねに最小要素をもつとき,
整列集合であるという.■
公理的集合論を踏まえた研究によって,20世紀に次の事実が発見された.
定理 2
集合の公理1.〜8.の下において,次の3命題は同値である.
- 選択公理が成立する.
- (ツォルンの補題)帰納的半順序集合には
極大要素が存在する.
- (整列可能定理)任意の集合は,
その上にある順序を定義して整列集合にすることができる.
■
この証明は例えば『集合論入門』[1]や『集合と位相』[25]にある.
この選択公理やツォルンの補題によって,それまでは成り立つはずだと証明なしに考えられてきた次のような多くの定理が,はじめて証明される.
- 任意の二つの集合の濃度は比較可能である.
これはいいかえると,任意の二つの集合において,
一方から他方の部分集合への一対一対応が存在する,ということである.
- 体上の線型空間には基が存在する.
- コンパクト空間の任意個の積空間はコンパクトである.
実はこれらの定理もまた,選択公理と同値であることが知られている.あるいは,
- すべての無限集合は,可算無限な濃度部分集合をもつ.
- 任意の体は,代数的閉包が存在する.
などもまた,選択公理を用いないで証明することは難しい.ただし,不可能性の証明までがなされているかどうかは,不知.
さらに驚くべきことに,次のことが示されている.
定理 3
- この同値な命題は,集合の公理1.〜8.と独立である.いいかえれば,集合の公理1.〜8.が矛盾を含んでいなければ,これに選択公理を付け加えても,あるいは選択公理の否定命題を付け加えても,やはり矛盾は起こらない.
■
※ 無矛盾性の証明はゲーデルによって,独立性の証明はコーエンによってなされた.
- 先に述べた一般連続体仮説について.集合の公理1.〜8.に一般連続体仮説を公理として加えると,選択公理が定理として示される.
■
※ これはシールピンスキによって示された.
- 一般連続体仮説は,集合の公理1.〜8.に選択公理を加えた公理系から独立である.
■
※これもまたゲーデルとコーエンによって示されている.
平行線の公理が,ユークリッド幾何の公理系のなかで独立しており,それを否定した公理を加えても,豊かな幾何,つまり非ユークリッド幾何があることが,19世紀に見出された.選択公理や,あるいは一般連続体仮説を否定した体系が豊かであるのか否か,それは開かれた問題である.
このように,19世紀から20世紀にかけて,人間が数学として考えるということの根底に,どのような仮説が存在しているのかが,解明されていった.
われわれが選択公理を,有限個の集合から選ぶことの一般化として考えるとき,そこで思い浮かべているのは可算無限個の集合から選ぶことである.しかし,選択公理は可算無限という制限を設けない.
選択公理を文字通り適用すると,次の定理が成り立つ.
定理 4 (バナッハ・タルスキーの定理)
大きさの異なる中身の詰まった2つの球(体)
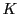
と
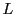
があるとする.このとき,
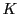
を適当に有限個に分割し, それらを再び寄せ集めることによって,
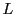
を作ることができる.
■
この定理の詳しい解説やその証明は,例えば
「バナッハ・タルスキーの定理」
等にある.しかしこれは決してパラドックスではない.任意の集合で選択公理が成り立つとしたその帰結である.
『解析概論』にもこのような事例はすでに紹介されている.たとえばPeanoの曲線がそうである.それは,区間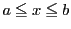 で定義された連続曲線
で定義された連続曲線
で,一定の平面領域の点をすべて通過するものである.それが具体的に構成されている.
これも一見不思議である.しかしこれもまた,実数と連続の定義からの帰結である.
われわれが採用した公理系は,ある理論を展開するのに必要な内容で構成されている.
数学の公理系というのは絶対のものではなく,それによって数学的対象を定義する.逆に言えば,数学的現象,数学的真理を記述する方法である.集合論の公理も数学の方法であり,基礎の方法として,数学の言葉である.
方法に絶対のものはなく,数学の発展とともに,方法もまた変化し発展する.今日の数学の新たな枠組みを作ったフランスを中心とする数学者集団ブルバキは,このことを端的に次のように述べる.
もし,未来にそれ(現在の数学の枠組みとなっている公理的集合論)が破綻しても数学は必ずや新しい基礎を見つけるだろう.
体系とは完結したものではなく,それ自体が開かれた発展する方法なのである.このような立場からいえば,解析の基礎を考え学ぶうえでは,このような矛盾の存在をおさえつつ,とりあえず素朴な集合論からはじめればよい.


 次: 整数の公理
上: 集合と公理
前: 対応と写像
次: 整数の公理
上: 集合と公理
前: 対応と写像
2014-05-23
を,それ自身を要素に含まない集合
の集合とする.つまり
![]() が
が![]() のときの意味は,
のときの意味は,![]() に属する集合が空でないとき,各
に属する集合が空でないとき,各![]() から
から![]() の要素を選ぶ関数が存在するということである.それを論理式に書くと次のようになる.
の要素を選ぶ関数が存在するということである.それを論理式に書くと次のようになる.
![]() で定義された連続曲線
で定義された連続曲線