


次: 条件の同値変形
上: 何をどう置くか
前: 何をどう置くか
三角形
ABC複素平面上におき,
A(z1),
B(z2),
C(z3)とする.
とし.
D(w1),
E(w2)とおく.
点
C ,点
D は直線
AB に関して反対側にあり,
また,点
B ,点
E は直線
AC に関して反対側にあるので,
である.点
M と
N に対応する複素数を 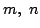 とすると
とすると
一方,
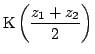 ,
,
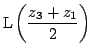 なので
なので
ここで
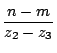 が純虚数になったので,
直線
MNと直線
BCが垂直であること
が示された.
が純虚数になったので,
直線
MNと直線
BCが垂直であること
が示された.
AozoraGakuen
2002-09-04
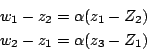
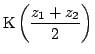 ,
,
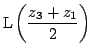 なので
なので
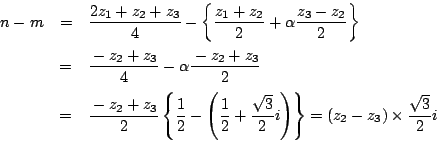
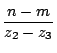 が純虚数になったので,
直線
MNと直線
BCが垂直であること
が示された.
が純虚数になったので,
直線
MNと直線
BCが垂直であること
が示された.