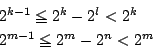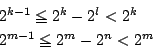次: 例で考える
上: 条件の同値変形
前: 条件の同値変形
-
- (1)
-
a と b がともに整数で b<a なので 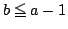 が成り立つ.
よって
が成り立つ.
よって
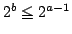 は成り立つ.
2b>0 より
2a-2b<2aも成立.
は成り立つ.
2b>0 より
2a-2b<2aも成立.
- (2)
- (1)から
2k-2l=2m-2nなので,
つまり
ゆえに
k-1<m<k+1
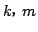 がともに整数なので k=m である.このとき
2k-2l=2m-2nよりl=nである.
別解
がともに整数なので k=m である.このとき
2k-2l=2m-2nよりl=nである.
別解
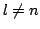 とする.l> n とすれば
2k-2l=2m-2nなので,
とする.l> n とすれば
2k-2l=2m-2nなので,
2k-n-2l-n=2m-n-1
右辺は奇数で左辺は偶数なので矛盾.
このとき
2k-2l=2m-2nより k=m .
l<n のときも同様である.
AozoraGakuen
2002-09-04