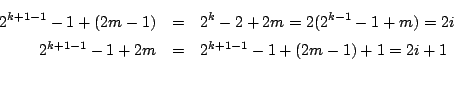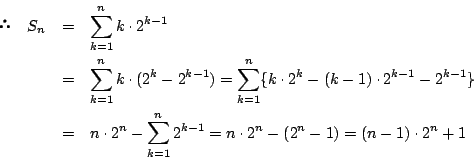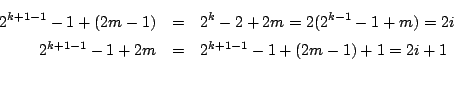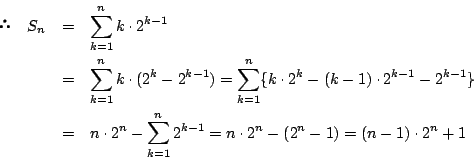次: 必要条件・十分条件 上: 例で考える 前: 例で考える

02滋賀医大

(1)

頂点 i が上から k 段目，左から m 番にあるとする． k 段目には 2^k-1 個の頂点があるので，

$$i=1+2+2^2+\cdots+2^{k-2}+m=2^{k-1}-1+m \quad \cdots\maru{1}$$

が成り立つ． このとき，頂点i のすぐ下の段にあって頂点 i と結ばれている頂点は， 上からk 段目，左から 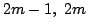$2m-1,\ 2m$ の2つである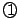． $\maru{1}$ の関係式の k と m に， k+1 と 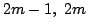$2m-1,\ 2m$ を代入する．

$$\begin{eqnarray*}2^{k+1-1}-1+(2m-1)&=&2^k-2+2m=2(2^{k-1}-1+m)=2i\\ 2^{k+1-1}-1+2m&=&2^{k+1-1}-1+(2m-1)+1=2i+1\\ \end{eqnarray*}$$

であるから，それらの頂点の番号は2i と 2i+1 である．

(2)

k 段目の石は k 回の操作で上がりになる．

$$\begin{eqnarray*}∴ \quad S_n&=&\sum_{k=1}^nk \cdot 2^{k-1}\\ &=&\sum_{k=1}^n... ...t 2^n-\sum_{k=1}^n2^{k-1}=n\cdot2^n-(2^n-1)=(n-1)\cdot2^n+1\\ \end{eqnarray*}$$

(3)

k 段目の出会うべき頂点の決め方は 2^k-1 通り． その各々について，第 k 段目のその頂点ではじめて出会うのは， その頂点の下にあるk+1 段目の隣りあう頂点に来ることである． k+1 段目の一つの頂点に来る n 段の頂点は 2^n-k-1 個あり， 頂点 i と頂点 j の決め方がそれぞれ 2^n-k-1通りである． ゆえに求める自然数の対 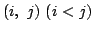$(i,\ j)\ (i<j)$ の個数は

$$2^{k-1}\times(2^{n-k-1})^2=2^{2n-k-3}\ (個)$$

である．