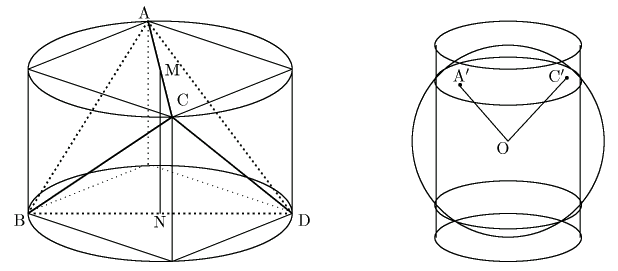
 明らかに線分
MNは辺
AC と辺
BDに
垂直である.直線
MNを回転軸にして直径 a の円柱を作ると
正四面体の各頂点がちょうど円柱の表面上にある.
したがって,a<bなら,直径が b の十分に長い円柱の内部に,
正四面体
ABCD をすっぽり入れることができる.ゆえに
a<bは十分条件である.
明らかに線分
MNは辺
AC と辺
BDに
垂直である.直線
MNを回転軸にして直径 a の円柱を作ると
正四面体の各頂点がちょうど円柱の表面上にある.
したがって,a<bなら,直径が b の十分に長い円柱の内部に,
正四面体
ABCD をすっぽり入れることができる.ゆえに
a<bは十分条件である.
なので矛盾である. ゆえにa<bは必要条件でもある. 求める条件はa<b.
 明らかに線分
MNは辺
AC と辺
BDに
垂直である.直線
MNを回転軸にして直径 a の円柱を作ると
正四面体の各頂点がちょうど円柱の表面上にある.
したがって,a<bなら,直径が b の十分に長い円柱の内部に,
正四面体
ABCD をすっぽり入れることができる.ゆえに
a<bは十分条件である.
明らかに線分
MNは辺
AC と辺
BDに
垂直である.直線
MNを回転軸にして直径 a の円柱を作ると
正四面体の各頂点がちょうど円柱の表面上にある.
したがって,a<bなら,直径が b の十分に長い円柱の内部に,
正四面体
ABCD をすっぽり入れることができる.ゆえに
a<bは十分条件である.