


次: 必要条件・十分条件
上: 例で考える
前: 例で考える
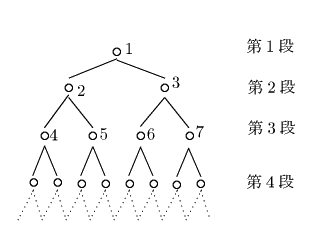 各頂点から2本ずつ枝分かれした樹形図の各頂点に,上から下へ左から右へと図のように番号をつけ
番号 i をつけた頂点を頂点 i と呼ぶ.
各頂点から2本ずつ枝分かれした樹形図の各頂点に,上から下へ左から右へと図のように番号をつけ
番号 i をつけた頂点を頂点 i と呼ぶ.
-
- (1)
- 頂点 i のすぐ下の段にあって頂点 i と結ばれている頂点の番号は
2i と 2i+1 であることを示せ.
- (2)
- 第 n 段までのすべての頂点に1つずつ石を置いて,各石を1段ずつ
枝に沿って上に動かし,頂点1に達すれば「上がり」として外に取り出す.
全ての石を取り出すのに要する操作の総数 Sn を求めよ.ただし,1つの
石を1段上に動かすこと,または頂点1にある石を外に取り出すことを1つの
操作とする.
たとえば,
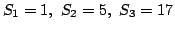 である.また,1つの頂点には2つ
以上の石は置けないものとする.
である.また,1つの頂点には2つ
以上の石は置けないものとする.
- (3)
- 自然数
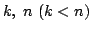 に対して,次のような条件を満たす自然数の対
に対して,次のような条件を満たす自然数の対
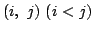 の個数を
の個数を 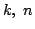 で表せ.
で表せ.
AozoraGakuen
2002-09-04
 各頂点から2本ずつ枝分かれした樹形図の各頂点に,上から下へ左から右へと図のように番号をつけ
番号 i をつけた頂点を頂点 i と呼ぶ.
各頂点から2本ずつ枝分かれした樹形図の各頂点に,上から下へ左から右へと図のように番号をつけ
番号 i をつけた頂点を頂点 i と呼ぶ.
 各頂点から2本ずつ枝分かれした樹形図の各頂点に,上から下へ左から右へと図のように番号をつけ
番号 i をつけた頂点を頂点 i と呼ぶ.
各頂点から2本ずつ枝分かれした樹形図の各頂点に,上から下へ左から右へと図のように番号をつけ
番号 i をつけた頂点を頂点 i と呼ぶ.
