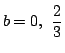 .
.
で, b=1 ならf(x)=1となる x は

と推測される.これを数学的帰納法で示す. n=1 のときは(1)より成立している. n=k のとき成立しているとする. n=k+1 のときの a2 がとりうる値は n=k のときのa1 がとりうる値に等しい.ゆえにn=k のときの仮定より
である.したがって
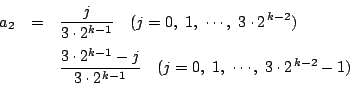
つまり
となり,n=k+1 でも成立する.
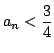 とする.
このときある番号 n で 初期値 a1 は(3)のいずれかに一致するものが
存在すること示せばよい.
つまりある番号 n0 で an0=0 または
とする.
このときある番号 n で 初期値 a1 は(3)のいずれかに一致するものが
存在すること示せばよい.
つまりある番号 n0 で an0=0 または
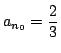 となるものが
存在すること示せばよい.
a1=0 なら存在した.
もし
となるものが
存在すること示せばよい.
a1=0 なら存在した.
もし
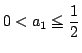 なら a2=2a1 と,
なら a2=2a1 と,
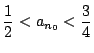 となるものがある.さらにこのとき
となるものがある.さらにこのとき
なので
である.したがって同様に
である.
である.ゆえにこの範囲の n に対しては漸化式 an+1=-2an+2 が成立する. これから
つまり
ここで
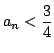 なので
なので
これから
これが
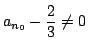 なら
なら
なので,十分大きい n で n-n0 が偶数になるものについては
が成立しない. ゆえに
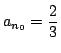 .つまり番号 n0 に対しan0 が(1)の値に一致した.
ゆえに a=1 は(3)の条件をみたすことになり,背理法が成立した.
.つまり番号 n0 に対しan0 が(1)の値に一致した.
ゆえに a=1 は(3)の条件をみたすことになり,背理法が成立した.
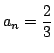 となる.つまり数列
となる.つまり数列 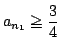 となるものがある.
このとき
an1+1=-2an1+2 より
となるものがある.
このとき
an1+1=-2an1+2 より
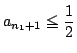 となる.
ここでもし n>n1 なる n に対してつねに
となる.
ここでもし n>n1 なる n に対してつねに
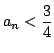 なら,(4)と同様の
議論によって,ある n0 で
なら,(4)と同様の
議論によって,ある n0 で
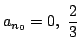 となるものがあり,
数列
となるものがあり,
数列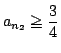 となるものがあり,
となるものがあり,
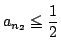 となる.
これをくり返せば,
となる.
これをくり返せば,
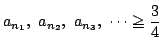 となるものが存在し,このとき
となるものが存在し,このとき
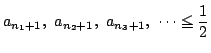 である.
つまり数列
である.
つまり数列 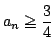 となるものと,
となるものと,
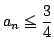 となるものが無数に存在する.
数列
となるものが無数に存在する.
数列