京大特色入試総人理系2番
$ y=\dfrac{1}{x} $ のとき, $ y'=-\dfrac{1}{x^2} $ なので,点 $ Q\left(\alpha,\ \dfrac{1}{\alpha} \right) $ での接線は
\[
y=-\dfrac{1}{\alpha^2}\left(x-\alpha \right)+\dfrac{1}{\alpha}=
-\dfrac{1}{\alpha^2}x+\dfrac{2}{\alpha}
\]
である.点 $ R $ についても同様で,それぞれ点 $ P $ を通るので,
\[
\begin{array}{l}
Y=-\dfrac{1}{\alpha^2}X+\dfrac{2}{\alpha}\\
Y=-\dfrac{1}{\beta^2}X+\dfrac{2}{\beta}
\end{array}
\]
が成り立つ.これより
\[
Y=\dfrac{2}{\beta+\alpha},\ X=\dfrac{2\alpha\beta}{\beta+\alpha}
\]
つまり,
\[
\alpha+\beta=\dfrac{2}{Y},\ \alpha\beta=\dfrac{X}{Y}
\]
である.
$ \tan\theta_1=-\dfrac{1}{\alpha^2} $ ,
$ \tan\theta_2=-\dfrac{1}{\beta^2} $ とおくと, $ 0< \alpha< \beta $ より
$ \theta_1 > \theta_2 $ で, $ \angle QPR=\dfrac{3}{4}\pi $ より,
\[
\tan\dfrac{3}{4}\pi=
\tan(\theta_1-\theta_2)=\dfrac{-\dfrac{1}{\alpha^2}+\dfrac{1}{\beta^2}}{1+\dfrac{1}{\alpha^2\beta^2}}
\]
より
\[
(\beta+\alpha)(\beta-\alpha)=\alpha^2\beta^2+1
\quad ………\cdots(1)
\]
ここで
\[
(\beta-\alpha)^2=(\beta+\alpha)^2-4\alpha\beta=\dfrac{4}{Y^2}-\dfrac{4X}{Y}=\dfrac{4(1-XY)}{Y^2}
\]
より, $ 0< \alpha< \beta $ とあわせて
\[
\beta-\alpha=\dfrac{2}{Y}\sqrt{1-XY}
\]
なので, $(1)$ から,
\[
\dfrac{4}{Y^2}\sqrt{1-XY}=\dfrac{X^2}{Y^2}+1
\]
である.つまり
\[
4\sqrt{1-XY}=X^2+Y^2
\quad ………(2)
\]
これが軌跡 $ \gamma $ の方程式である.
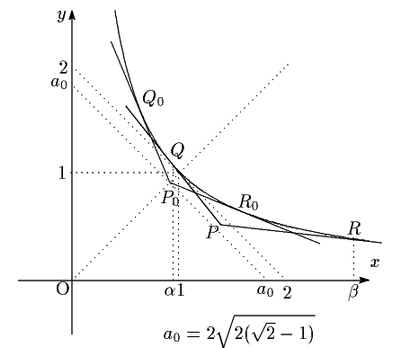
問2 図のように $ C $ 上の点 $ (1,\ 1) $ での接線は $ x+y=2 $ である.
$ \gamma $ 上の点 $ P(X,\ Y) $ は $ x+y< 2 $ で定まる領域内にある.
なぜなら,接線の傾きは $ -1=\tan\dfrac{3}{4}\pi $ であるから,
点 $ P $ が領域 $ x+y\geqq 2 $ にあれば,直線 $ PQ $ の傾きは $ -1 $ より大きい負の値をとり,
直線 $ PR $ の傾きも負となるので, $ \angle QPR > \dfrac{3}{4}\pi $ となるからである.
次に, $ \gamma $ 上の点 $ P(X,\ Y) $ で $ X=Y $ であるものを $ P_0 $ とする.
$(2)$ より,
\[
4\sqrt{1-X^2}=2X^2
\]
$ X > 0 $ でこれを解いて $ X=Y=\sqrt{2(\sqrt{2}-1)} $ となる.
$ P_0 $ を通る傾き $ -1 $ の直線は $ x+y=2\sqrt{2(\sqrt{2}-1)} $ である.
次に,軌跡 $ \gamma $ は不等式 $ x+y \geqq 2\sqrt{2(\sqrt{2}-1)} $ で定まる領域内にあることを示す.
そのために,軌跡 $ \gamma $ を原点の周りに $ \dfrac{\pi}{4} $ 回転する.
$ \gamma $ 上の点 $ (X,\ Y) $ がこの回転で $ (s,\ t) $ に移るとする.
$ (s,\ t) $ を $ -\dfrac{\pi}{4} $ 回転した点が $ (X,\ Y) $ なので,これを複素数平面で考えて,
\[
X+iY=\left\{\cos\left(-\dfrac{\pi}{4}\right)+i\sin\left(-\dfrac{\pi}{4}\right)\right\}(s+it)
=\dfrac{1-i}{\sqrt{2}}(s+it)
\]
である.これから, $ X=\dfrac{s+t}{\sqrt{2}} $ ,
$ Y=\dfrac{-s+t}{\sqrt{2}} $ である.
これを $ \gamma $ の方程式 $(2)$ に代入して,
\[
4\left(1-\dfrac{t^2-s^2}{2} \right)^{\frac{1}{2}}
=s^2+t^2
\]
これから
\[
2\sqrt{2}\left(2-t^2+s^2\right)^{\frac{1}{2}}=s^2+t^2
\]
この $ t $ を $ s $ の関数と見て, $ s $ に対する $ t $ の増減を調べる.
そのために両辺を $ s $ で微分する. $ \dfrac{dt}{ds}=t' $ と表す.
\[
\sqrt{2}\left(2-t^2+s^2\right)^{-\frac{1}{2}}(-2tt'+2s)=2s+2tt'
\]
これより,
\[
tt'=\dfrac{\sqrt{2}-\sqrt{2-t^2+s^2}}{\sqrt{2}+\sqrt{2-t^2+s^2}}\cdot s
\]
である. $ \gamma $ を回転した曲線は $ X > 0,\ Y > 0 $ より
$ -t< s< t $ ,つまり $ s^2< t^2 $ である.よって
$ \dfrac{\sqrt{2}-\sqrt{2-t^2+s^2}}{\sqrt{2}+\sqrt{2-t^2+s^2}} > 0 $ でかつ $ t > 0 $ なので,
$ t' $ は $ s=0 $ でのみ0となり,ここで負から正に変わる.
つまりここで極小で最小である.
これは,もとの軌跡 $ \gamma $ についてみれば,
$ \gamma $ が不等式 $ x+y \geqq 2\sqrt{2(\sqrt{2}-1)} $ で定まる領域内にあることを示している.
よって $ \gamma $ は2つの直線で定まる領域
\[
2\sqrt{2(\sqrt{2}-1)}\leqq x+y< 2(等号はX=Yのときのみ)
\]
にある.この結果,
軌跡 $ \gamma $ , $ x $ 軸の $ x\geqq 0 $ なる部分, $ y $ 軸の $ y\geqq 0 $ なる部分の3つで囲まれる図形の面積を $ S $ は
$ x $ 軸の $ x\geqq 0 $ なる部分, $ y $ 軸の $ y\geqq 0 $ なる部分とこれらの2直線でできる2つの三角形の面積に挟まれることを示している.
\[
\dfrac{1}{2}\cdot \left\{2\sqrt{2(\sqrt{2}-1)}\right\}^2
=4(\sqrt{2}-1)
\]
なので,
\[
4(\sqrt{2}-1)< S< 2
\]
が成り立つ.