阪大理系4番
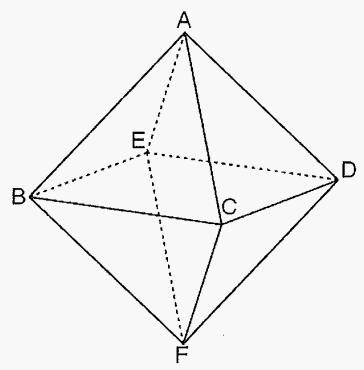
座標空間に6点 \[ \mathrm{A}(0,0,1),\mathrm{B}(1,0,0),\mathrm{C}(0,1,0),\mathrm{D}(-1,0,0),\mathrm{E}(0,-1,0), \mathrm{F}(0,0,-1) \] を頂点とする正八面体 $ \mathrm{ABCDEF} $ がある. $ s $ , $ t $ を $ 0< s< 1 $ , $ 0< t< 1 $ を満たす実数とする. 線分 $ \mathrm{AB} $ , $ \mathrm{AC} $ をそれぞれ $ 1-s:s $ に内分する点を $ \mathrm{P} $ , $ \mathrm{Q} $ とし. 線分 $ \mathrm{FD} $ , $ \mathrm{FE} $ をそれぞれ $ 1-t:t $ に内分する点を $ \mathrm{R} $ , $ \mathrm{S} $ とする.
(1) 4点 $ \mathrm{P},\ \mathrm{Q},\ \mathrm{R},\ \mathrm{S} $ が同一平面上にあることを示せ.
(2) 線分 $ \mathrm{PQ} $ の中点を $ \mathrm{L} $ とし,線分 $ \mathrm{RS} $ の中点を $ \mathrm{M} $ とする.
$ s $ , $ t $ が $ 0< s< 1 $ , $ 0< t< 1 $ の範囲を動くとき,線分 $ \mathrm{LM} $ の長さの最小値 $ m $ を求めよ.
(3) 正八面体 $ \mathrm{ABCDEF} $ の4点 $ \mathrm{P},\ \mathrm{Q},\ \mathrm{R},\ \mathrm{S} $
を通る平面による切り口の面積を $ X $ とする.線分 $ \mathrm{LM} $ の長さが(2)の値 $ m $ をとるとき,
$ X $ を最大とするような $ s $ , $ t $ の値と,そのときの $ X $ の値を求めよ.