京大理系6番文系4番解答
(1) 4頂点 $\mathrm{A,B,C,D}$の位置ベクトルを $ \overrightarrow{a},\ \overrightarrow{b},\ \overrightarrow{c},\ \overrightarrow{d} $ とおく.条件 $\mathrm{AC}=\mathrm{BD}$,$\mathrm{AD}=\mathrm{BC}$ より, \[ |\overrightarrow{c}-\overrightarrow{a}|=|\overrightarrow{d}-\overrightarrow{b}|,\ |\overrightarrow{d}-\overrightarrow{a}|=|\overrightarrow{c}-\overrightarrow{b}| \] 両辺の平方をとり,辺々加えて整理することにより \[ |\overrightarrow{a}|^2-\overrightarrow{a}\cdot\overrightarrow{c}-\overrightarrow{a}\cdot\overrightarrow{d}= |\overrightarrow{b}|^2-\overrightarrow{b}\cdot\overrightarrow{c}-\overrightarrow{b}\cdot\overrightarrow{d} \] つまり, \[ \overrightarrow{a}\cdot(\overrightarrow{a}-\overrightarrow{c}-\overrightarrow{d})= \overrightarrow{b}\cdot(\overrightarrow{b}-\overrightarrow{c}-\overrightarrow{d}) \quad \cdots(1) \] である. $\mathrm{P}$ と $\mathrm{Q}$ の位置ベクトルも同様におく. \[ \overrightarrow{p}=\dfrac{1}{2}\left(\overrightarrow{a}+\overrightarrow{b}\right),\ \overrightarrow{q}=\dfrac{1}{2}\left(\overrightarrow{c}+\overrightarrow{d}\right) \] なので, $ (1) $ より, \begin{eqnarray*} \overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{PQ}}&=& \left(\overrightarrow{b}-\overrightarrow{a} \right)\cdot \dfrac{1}{2}\left(\overrightarrow{c}+\overrightarrow{d}-\overrightarrow{a}-\overrightarrow{b}\right)\\ &=&\dfrac{1}{2}\overrightarrow{b}\cdot(\overrightarrow{c}+\overrightarrow{d}-\overrightarrow{b}) -\overrightarrow{a}\cdot(\overrightarrow{c}+\overrightarrow{d}-\overrightarrow{a})=0 \end{eqnarray*} つまり,辺 $\mathrm{AB}$ と線分 $\mathrm{PQ}$ は垂直である.
別解
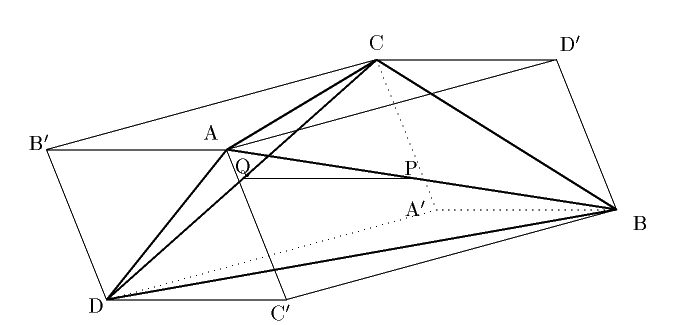
四面体 $\mathrm{ABCD}$ を,次のように平行六面体に埋め込む.
四面体 $\mathrm{ABCD}$ の重心を $\mathrm{G}$ とする.その位置ベクトルは
\[
\overrightarrow{g}
=\dfrac{1}{4}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{d})
\]
となる.
ここで,四面体 $ \mathrm{ABCD} $ で,各頂点 $ \mathrm{A},\ \mathrm{B},\ \mathrm{C},\ \mathrm{D} $
と,それらの重心に関する対称点を
$ \mathrm{A'},\ \mathrm{B'},\ \mathrm{C'},\ \mathrm{D'} $ とする.
改めて,基準点を重心にとり直す.4頂点 $ \mathrm{A},\ \mathrm{B},\ \mathrm{C},\ \mathrm{D} $ の位置ベクトルを
$ \overrightarrow{a},\ \overrightarrow{b},\ \overrightarrow{c},\ \overrightarrow{d} $ とすると,
\[
\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{d}=0
\]
で,
$ \mathrm{A'},\ \mathrm{B'},\ \mathrm{C'},\ \mathrm{D'} $ の位置ベクトルは
$ -\overrightarrow{a},\ -\overrightarrow{b},\ -\overrightarrow{c},\ -\overrightarrow{d} $ となる.
\begin{eqnarray*}
\overrightarrow{\mathrm{AC'}}&=&-\overrightarrow{c}-\overrightarrow{a}\\
\overrightarrow{\mathrm{D'B}}
&=&\overrightarrow{b}+\overrightarrow{d}=-\overrightarrow{c}-\overrightarrow{a}\\
\overrightarrow{\mathrm{CA'}}
&=&-\overrightarrow{a}-\overrightarrow{c}=-\overrightarrow{c}-\overrightarrow{a}\\
\overrightarrow{\mathrm{B'D}}
&=&\overrightarrow{d}+\overrightarrow{b}=-\overrightarrow{c}-\overrightarrow{a}
\end{eqnarray*}
つまり
\[
\overrightarrow{\mathrm{AC'}}=\overrightarrow{\mathrm{D'B}}=
\overrightarrow{\mathrm{CA'}}=\overrightarrow{\mathrm{B'D}}
\]
他も同様なので,四面体 $\mathrm{ABCD}$ は平行六面体 $ \mathrm{AC'BD'DA'CB'} $
に埋め込まれていいる.
(2)
線分PQを軸とする空間図形の180°の回転を考える.
回転は合同な変換である.
(1)と同様に,線分 $ \mathrm{PQ}$ は辺 $ \mathrm{CD}$とも直交している.
よって,この回転によって頂点 $ \mathrm{A}$ は $ \mathrm{B}$ , $ \mathrm{B}$ は $ \mathrm{A}$ に移り,
頂点 $ \mathrm{C}$ は $ \mathrm{D}$ , $ \mathrm{D}$ は $ \mathrm{C}$ に移る.
つまりこの回転によって,四面体 $ \mathrm{ABCD}$ は頂点と辺が入れ変わり,四面体としてはそれ自身に移る.
一方,平面 $ \alpha $ もそれ自身に移り,
平面 $ \alpha $ によって分けられる空間の2つの領域は,互いに入れ替わる.
よって,平面 $ \alpha $ で四面体 $ \mathrm{ABCD}$ を切って2つの部分に分けるとき,
その2つの領域はこの回転で互いに入れ替わる.
つまり,2つの部分の体積は等しい.