京大特色1番
凸五角形 $ \mathrm{A}_n\mathrm{B}_n\mathrm{C}_n\mathrm{D}_n\mathrm{E}_n\ (n=1,\ 2,\ \cdots) $
が次の条件を満たしている.
\[
\begin{array}{l}
\mathrm{A}_{n+1}は\mathrm{C}_n\mathrm{D}_nの中点\\
\mathrm{B}_{n+1}は\mathrm{D}_n\mathrm{E}_nの中点\\
\mathrm{C}_{n+1}は\mathrm{E}_n\mathrm{A}_nの中点\\
\mathrm{D}_{n+1}は\mathrm{A}_n\mathrm{B}_nの中点\\
\mathrm{E}_{n+1}は\mathrm{B}_n\mathrm{C}_nの中点
\end{array}
\]
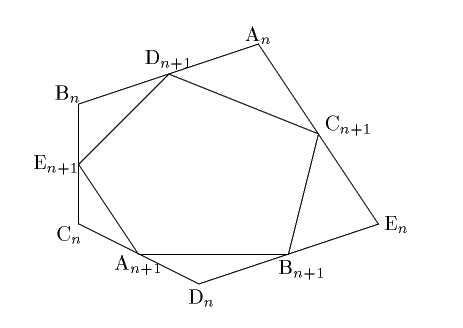
下図は,五角形 $ \mathrm{A}_n\mathrm{B}_n\mathrm{C}_n\mathrm{D}_n\mathrm{E}_n $ と五角形
$ \mathrm{A}_{n+1}\mathrm{B}_{n+1}\mathrm{C}_{n+1}\mathrm{D}_{n+1}\mathrm{E}_{n+1} $ の位置関係を図示したものである.
以下の設問に答えよ.
(1) 正の実数 $ \alpha $ をうまく取ると, 数列 $ \left\{\alpha^n\left|\overrightarrow{\mathrm{A}_n\mathrm{B}_n} \right|\right\} $ が0でない実数に収束するようにできることを示せ.
(2) 五角形 $ \mathrm{A}_n\mathrm{B}_n\mathrm{C}_n\mathrm{D}_n\mathrm{E}_n $ の5本の辺の長さの和を $ L_n $ ,5本の対角線の長さの和を $ M_n $ とする. 極限値 $ \displaystyle \lim_{n \to \infty}\dfrac{M_n}{L_n} $ を求めよ.
ただし,五角形が凸であるとは,その内角かすべて $ 180^{\circ} $ 未満であることをいう.また, 五角形の対角線とは,2頂点を結ぶ線分で辺でないもののことである.