東工大1番解答
(1) 方程式①が実数解を持たないとき，その解は互いに共役である． それを$\alpha$，$\overline{\alpha}$ とする．解と係数の関係より \[ \alpha\overline{\alpha}=|\alpha|^2=1 \] となり，①の2解は原点を中心とする半径1の円周上，実軸に関して対称の位置にある． 同様に，②の2解を $\beta$，$\overline{\beta}$ とすると， $|\beta|^2=2$となり，2解は原点を中心とする半径$\sqrt{2}$の円周上に，実軸に関して対称の位置にある．
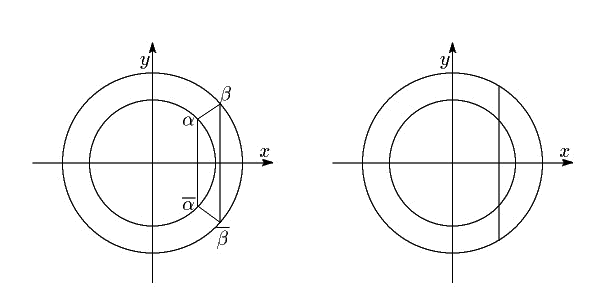
$\alpha+\overline{\alpha}=-a$， $\beta+\overline{\beta}=-b$ なので，この条件は$a=b$である．
$a\ne b$ のとき，同一直線上にない．このときは，対称性から4つの解が作る四辺形は等脚台形である． 向かい合う内角の和が $\pi$ となるので，4つの解はすべて同一円周上にある．
その中心は実数で，これを $x$ とすると， \[ |\alpha-x|^2=|\beta-x|^2 \] より， \[ (\alpha-x)(\overline{\alpha}-x)=(\beta-x)(\overline{\beta}-x) \] これから \[ \alpha\overline{\alpha}-(\alpha+\overline{\alpha})x= \beta\overline{\beta}-(\beta+\overline{\beta})x \] つまり， \[ 1+ax=2+bx \] $a-b\ne 0$ なので， \[ x=\dfrac{1}{a-b} \] である．また半径を $r$ とすると， \begin{eqnarray*} r^2&=&\left|\alpha-x\right|^2=\alpha\overline{\alpha}-(\alpha+\overline{\alpha})x+x^2\\ &=&1-\dfrac{-a}{a-b}+\dfrac{1}{(a-b)^2}=\dfrac{2a^2-3ab+b^2+1}{(a-b)^2} \end{eqnarray*} よって， \[ r=\dfrac{\sqrt{2a^2-3ab+b^2+1}}{|a-b|} \] となる．
(2)
3つの方程式①，②，③がいずれも実数解を持たない条件は，
それらの判別式が負なので，
\[
a^2-4< 0,\
b^2-8< 0,\
c^2-12< 0
\]
つまり
\[
|a|< 2,\
|b|< 2\sqrt{2},\
|c|< 2\sqrt{3}
\]
である．かつ，それらの解がいずれの組も同一直線上にない条件は，
\[
a\ne b,\ b\ne c,\ c\ne a
\]
である．このとき，すべて同一円周上にあるための条件は，中心が一致するときときである．
②，③の4解のある円の中心を $y$ とすると，同様に考え，
\[
2+by=3+cy
\]
がなり立ち，これより，$y=\dfrac{1}{b-c}$ なので，中心が一致する条件は
\[
\dfrac{1}{a-b}=\dfrac{1}{b-c}
\]
より $a-b=b-c$．つまり
\[
a+c=2b
\]
である．
条件 $2b=a+c$ のもとで，$b=a$ または $b=c$ なら $c=a$ となるので，対偶をとり，
$c\ne a$ かつ $2b=a+c$ なら， $b\ne a$ と $b\ne c$ はなり立つ．
また $|a|<2$，$|c|<2\sqrt{3}$ なら
\[
|b|=\left|\dfrac{a+c}{2}\right|\leqq \dfrac{|a|+|c|}{2}< \dfrac{2+2\sqrt{3}}{2}=1+\sqrt{3}
\]
で，
\[
1+\sqrt{3}< 2.8< 2\sqrt{2}
\]
なので， $|b|<2\sqrt{2}$ はなりたつ．
よって，
\[
a\ne c,\ |a|< 2,\ |c|< 2\sqrt{3},\ 2b=a+c
\]
であれば，すべての条件がなりたつ．
逆にこのいずれもが必要なので，これが求める必要十分条件である．