千葉大11番解答
(1) \[ 0\leqq f_n(x)\leqq 1 (0\leqq x\leqq 1) \quad \cdots① \] を, $ n $ に関する数学的帰納法で示す. $ f_1(x)=0 $ より $ n=1 $ のとき成立する. $ n $ のとき成立するとする. $ 0\leqq f_n(x)\leqq 1 $ より $ -1\leqq f_n(x)-1\leqq 0 $ なので, $ \left\{f_n(x)-1 \right\}^2\leqq 1 $ である.よって \[ f_{n+1}(x)=\int_0^x\left(f_n(t)-1 \right)^2\,dt \leqq \int_0^x1\,dt=x\leqq 1 \] より成立する.よってすべての自然数 $ n $ で $ ① $ が成立する.
(2) この不等式は, $ 0\leqq x\leqq 1 $ のとき, $ n $ が偶数なら $ f_n(x)\geqq f(x) $ , $ n $ が奇数なら $ f_n(x)\leqq f(x) $ を意味する. $ 0\leqq x\leqq 1 $ のとき, $ 0\leqq f(x) \leqq \dfrac{1}{2} $ である. よって, $ n=1 $ のときは, $ f_1(x)=0 $ より, $ f_1(x)\leqq f(x) $ は成立する. 従って, $ f_n(x)\geqq f(x) $ なら $ f_{n+1}(x)\leqq f(x) $ , $ f_n(x)\leqq f(x) $ なら $ f_{n+1}(x)\geqq f(x) $ を示せばよい. $ f_n(x)\geqq f(x) $ のとき, \[ 0\geqq f_n(x)-1\geqq f(x)-1 \] よって, \[ \{f_n(x)-1\}^2\leqq \{f(x)-1\}^2 \] したがって \begin{eqnarray*} f_{n+1}(x)&=&\int_0^x\left\{f_n(t)-1 \right\}^2\,dt\leqq \int_0^x\{f(t)-1\}^2\,dt\\ &=&\int_0^x\left(\dfrac{-1}{t+1}\right)^2\,dt=\biggl[-\dfrac{1}{t+1}\biggr]_0^x=\dfrac{x}{x+1}=f(x) \end{eqnarray*} $ f_n(x)\leqq f(x) $ のとき, \[ -1\leqq f_n(x)-1\leqq f(x)-1 \] よって, \[ \{f_n(x)-1\}^2\geqq \{f(x)-1\}^2 \] したがって同様に, \[ f_{n+1}(x)=\int_0^x\left\{f_n(t)-1 \right\}^2\,dt\geqq \int_0^x\{f(t)-1\}^2\,dt=f(x) \] よって,(2)の不等式が示された.
(3) \begin{eqnarray*} f_{n+1}(x)-f(x)&=&\int_0^x\left\{f_n(t)-1 \right\}^2\,dt-\int_0^x\left\{f(t)-1 \right\}^2\,dt\\ &=&\int_0^x\left\{f_n(t)+f(t)-2\right\}\left\{f_n(t)-f(t)\right\}\,dt \end{eqnarray*} ここで, $ 0\leqq t\leqq x\leqq 1 $ において, $ f_n(t)+f(t)-2\leqq 0 $ であり, $ f_n(t)-f(t) $ はつねに0以上か,0以下で符号の変化はない.よって, \[ \left|\int_0^x\left\{f_n(t)+f(t)-2\right\}\left\{f_n(t)-f(t)\right\}\,dt \right| = \int_0^x\left|f_n(t)+f(t)-2\right|\left|f_n(t)-f(t)\right|\,dt \] つまり, \[ \left|f_{n+1}(x)-f(x) \right|=\int_0^x\left|f_n(t)+f(t)-2\right|\left|f_n(t)-f(t)\right|\,dt \] がなりたつ. ここで, $ \displaystyle f_2(x)=\int_0^x(0-1)^2\,dt=x $ なので, \begin{eqnarray*} \left|f_1(x)-f(x) \right|&=&\left|\dfrac{x}{x+1}\right|\leqq x \\ \left|f_2(x)-f(x) \right|&=&\left|x-f(x)\right|=\left|\dfrac{x^2}{x+1}\right|\leqq \dfrac{x^2}{2} \end{eqnarray*} である.実際, $ 0\leqq x\leqq 1 $ において, \begin{eqnarray*} &&\dfrac{x^2}{x+1}\leqq\dfrac{x^2}{2}\\ &\iff&2x^2\leqq x^3+x\\ &\iff&0\leqq x(x-1)^2 \end{eqnarray*} である.これより \[ \left|f_n(x)-f(x) \right|\leqq \dfrac{x^n}{n} \] の成立を推測し,これを数学的帰納法で示す. $ n $ のとき成立するとする. $ \left|f_n(t)+f(t)-2\right|\leqq 2 $ であるから, \begin{eqnarray*} \left|f_{n+1}(x)-f(x) \right|&=&\int_0^x\left|f_n(t)+f(t)-2\right|\left|f_n(t)-f(t)\right|\,dt\\ &\leqq &\int_0^x2\cdot\dfrac{t^n}{n}\,dt =\biggl[\dfrac{2t^{n+1}}{n(n+1)}\biggr]_0^x=\dfrac{2x^{n+1}}{n(n+1)} \end{eqnarray*} $ n\geqq 2 $ のとき, \[ \dfrac{2x^{n+1}}{n(n+1)}\leqq\dfrac{x^{n+1}}{n+1} \] なので成立する.よって, $ 0\leqq a \leqq 1 $ の任意の $ a $ に対して, \[ \left|f_n(a)-f(a) \right|\leqq \dfrac{a^n}{n}\leqq \dfrac{1}{n} \] よって, $ \displaystyle \lim_{n \to \infty}\dfrac{1}{n}=0 $ より, \[ \lim_{n \to \infty}f_n(a)=f(a)=\dfrac{a}{a+1} \] である.
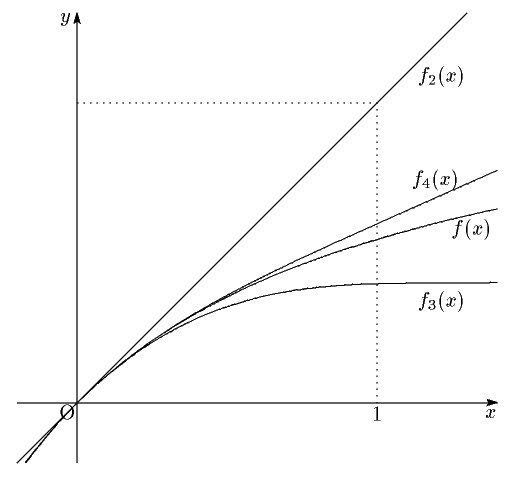
※ 参考までに. \begin{eqnarray*} f_2(x)&=&x\\ f_3(x)&=&\int_0^x(t-1)^2\,dt=\dfrac{(x-1)^3+1}{3}\\ f_4(x)&=&\int_0^x\left\{\dfrac{(t-1)^3+1}{3}-1 \right\}^2\,dt\\ &=&\dfrac{1}{63}\left\{(x-1)^7-7(x-1)^4+28x+8\right\} \end{eqnarray*} これをグラフに書くと次のようになる.