東大理科第6問解答
(1)
$ f(\theta)=A\sin 2\theta-\sin(\theta+\alpha) $ とおく.
$ 0\leqq \theta< 2\pi $ の範囲で
$ \sin 2\theta=1 $ となるのは, $ \theta=\dfrac{\pi}{4},\ \dfrac{5\pi}{4} $ のときであり,
$ \sin 2\theta=-1 $ となるのは, $ \theta=\dfrac{3\pi}{4},\ \dfrac{7\pi}{4} $ のときである.
よって $ A >1 $ なら, $ \alpha $ にかかわらず
\[
f\left(\dfrac{\pi}{4} \right)=A-\sin\left(\dfrac{\pi}{4}+\alpha\right) >0
\]
であり,同様にして,
\[
f\left(\dfrac{\pi}{4} \right) >0,\
f\left(\dfrac{3\pi}{4} \right)< 0,\
f\left(\dfrac{5\pi}{4} \right) >0,\
f\left(\dfrac{7\pi}{4} \right)< 0
\]
となる. $ f(\theta) $ は連続関数なので,中間値の定理により
$ f(\theta)=0 $ となる $ \theta $ が,区間
\[
\left(\dfrac{\pi}{4},\ \dfrac{3\pi}{4} \right),\ \quad
\left(\dfrac{3\pi}{4},\ \dfrac{5\pi}{4} \right),\ \quad
\left(\dfrac{5\pi}{4},\ \dfrac{7\pi}{4} \right)
\]
に存在する.
$ f(0)=f(2\pi)=-\sin\alpha $ である.
$ \sin\alpha= 0 $ のときは,
$ f(\theta)=0 $ の解として $ \theta=0 $ が加わる.
$ \sin\alpha\ne 0 $ のときは, $ \sin\alpha >0 $ か $ \sin\alpha< 0 $ に応じて,
区間 $ \left(0,\ \dfrac{\pi}{4} \right) $ または
区間 $ \left(\dfrac{7\pi}{4},\ 2\pi \right) $ に,
$ f(\theta)=0 $ となる $ \theta $ が存在する.
よって, $ A >1 $ のとき, $ f(\theta)=0 $ となる $ \theta $ が $ 0\leqq \theta< 2\pi $ の範囲に少なくとも4個存在する.
(2) 楕円 $ C $ 上の点 $ \mathrm{Q} $ を $ \mathrm{Q}\left(\sqrt{2}\cos\theta,\ \sin\theta \right) $ とおく.
点 $ \mathrm{Q} $ での接線は
\[
\dfrac{\sqrt{2}\cos\theta}{2}x+(\sin\theta)y=1
\]
である.領域 $ D $ の点 $ (x,\ y) $ をとる.
\[
\overrightarrow{\mathrm{QP}}=(x-\sqrt{2}\cos\theta,\ y-\sin\theta)
\]
が接線と直交しているので,接線の法線方向 $ \left(\dfrac{\sqrt{2}\cos\theta}{2},\ \sin\theta \right) $
と平行である.2ベクトルの平行条件から
\[
(x-\sqrt{2}\cos\theta)\sin\theta-(y-\sin\theta)\cdot\dfrac{\sqrt{2}\cos\theta}{2}=0
\]
である.これを整理して,
\[
\dfrac{\sqrt{2}}{4}\sin2\theta-\left(x\sin\theta+\dfrac{\sqrt{2}}{2}y\cos\theta\right)=0
\quad \cdots ①
\]
となる.さらに,
\[
x\sin\theta+\dfrac{\sqrt{2}}{2}y\cos\theta=
\sqrt{x^2+\dfrac{y^2}{2}}\sin(\theta+\alpha)
\]
とおく,
\[
\dfrac{\sqrt{2}}{4}\sin2\theta
-\sqrt{x^2+\dfrac{y^2}{2}}\sin(\theta+\alpha)=0
\]
となる $ \theta $ が $ 0\leqq \theta< 2\pi $ の範囲に少なくとも4個あるような $ r $ の条件が求めるものである.
$ x=y=0 $ のときは $ \theta=0,\ \dfrac{\pi}{2},\ \pi,\ \dfrac{3\pi}{2} $ の4個ある.
以下, $ x^2+\dfrac{y^2}{2}\ne 0 $ とする.
このとき,(1)から
\[
\dfrac{\dfrac{\sqrt{2}}{4}}{\sqrt{x^2+\dfrac{y^2}{2}}} >1
\]
であれば少なくとも4個存在する.
これを整理して,
\[
2x^2+y^2< \dfrac{1}{4}
\]
は十分条件である.よって $ r^2\leqq \dfrac{1}{4} $ ,
つまり $ r\leqq \dfrac{1}{2} $ は十分条件である.
$ r>\dfrac{1}{2} $ とする.このときは
\[
2x^2+y^2=\dfrac{1}{4}
\]
となる $ x $ と $ y $ がとれる.これを満たす組として
$ (x,\ y)=\left(\dfrac{1}{4},\ \dfrac{\sqrt{2}}{4} \right) $ を用いると,
$ ① $ は
\[
\dfrac{1}{4}\left(\sqrt{2}\sin2\theta-\sin\theta-\cos\theta\right)=0
\]
となる. $ \sqrt{2}\sin2\theta-\sin\theta-\cos\theta=0 $ となる $ \theta $ を考えるため
ここで, $ \sqrt{2}\sin2\theta $ と $ \sin\theta+\cos\theta=\sqrt{2}\sin\left(\theta+\dfrac{\pi}{4} \right) $ のグラフを描くと次のようになる.
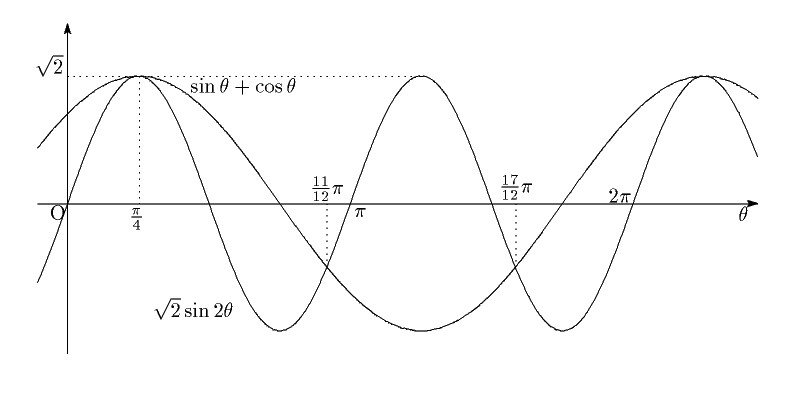
\[
\sin2\theta-\sin\left(\theta+\dfrac{\pi}{4} \right)
=2\cos\dfrac{3\theta+\dfrac{\pi}{4}}{2}\sin\dfrac{\theta-\dfrac{\pi}{4}}{2}=0
\]
を解いて,
\[
\dfrac{3\theta+\dfrac{\pi}{4}}{2}=\dfrac{\pi}{2},\ \dfrac{3\pi}{2},\ \dfrac{5\pi}{2},\
\dfrac{\theta-\dfrac{\pi}{4}}{2}=0
\]
より
\[
\theta=\dfrac{\pi}{4}\ (重解),\ \dfrac{11}{12}\pi,\ \dfrac{17}{12}\pi
\]
となる.
$ 0\leqq \theta< 2\pi $ の範囲の $ \theta $ は3個である.
$ r >\dfrac{1}{2} $ のとき反例ができたので, $ r\leqq \dfrac{1}{2} $ は必要条件でもある.
よって, $ r $ の最大値は $ \dfrac{1}{2} $ である.
※ 注意
本問は4本以上の法線が引ける点であるための十分条件を求めている.
$ r $ の最大値とはいえ,この形での最大値である.
では必要十分条件はどのようになるのか.
必要十分条件
$ a $ と $ b $ を $ a>b $ の正の定数とする $ xy $ 平面上に楕円 $ C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 $ がある.
平面上の点 $ \mathrm{P} $ から少なくとも4本の異なる法線が引けるとする.
このような点 $ \mathrm{P} $ の集合は,不等式
$ (ax)^{\frac{2}{3}}+(by)^{\frac{2}{3}}< (a^2-b^2)^{\frac{2}{3}} $
で表される領域となる.
証明
$ C $ 上の点 $ \mathrm{Q}(a\cos\theta,\ b\sin\theta) $ での $ C $ の接線は
\[
\dfrac{\cos\theta}{a}x+\dfrac{\sin\theta}{b}y=1
\]
である。その法線方向が $ \left(\dfrac{\cos\theta}{a},\ \dfrac{\sin\theta}{b} \right) $ である。
$ \overrightarrow{\mathrm{PQ}}=(a\cos\theta-X,\ b\sin\theta-Y) $ がこの法線方向と平行であるので,
\[
\dfrac{\cos\theta}{a}\left(b\sin\theta-Y \right)-
\dfrac{\sin\theta}{b}\left(a\cos\theta-X \right)=0
\quad \cdots②
\]
$ 0< \theta< 2\pi,\ \theta\ne \dfrac{\pi}{2},\ \pi,\ \dfrac{3\pi}{2} $ なので,
\[
a^2-b^2=\dfrac{aX}{\cos\theta}-\dfrac{bY}{\sin\theta}
\]
がなりたつ.
$ X >0,\ Y >0 $ とする。
このとき,点 $ \mathrm{P}(X,\ Y) $ を通る法線となる $ C $ 上の点を $ (a\cos\theta,\ b\sin\theta) $
とすると, $ \theta\ne 0,\ \dfrac{\pi}{2},\ \pi,\ \dfrac{3\pi}{2} $ である。
$ 0<\theta<2\pi,\ \theta\ne \dfrac{\pi}{2},\ \pi,\ \dfrac{3\pi}{2} $ に対して,
$ f(\theta)=\dfrac{aX}{\cos\theta}-\dfrac{bY}{\sin\theta} $ とおく。
\begin{eqnarray*}
f'(\theta)&=&\dfrac{\sin\theta}{\cos^2\theta}aX+\dfrac{\cos\theta}{\sin^2\theta}bY\\
&=&\dfrac{aX\sin^3\theta+bY\cos^3\theta}{\sin^2\theta\cos^2\theta}
\end{eqnarray*}
$ f'(\theta)=0 $ となる $ \theta $ は
$ \dfrac{\sin^3\theta}{\cos^3\theta}=-\dfrac{bY}{aX} $ となるとき,つまり,
$ \tan\theta=-\left(\dfrac{bY}{aX} \right)^{\frac{1}{3}} $ のときである。
$ -\left(\dfrac{bY}{aX} \right)^{\frac{1}{3}}<0 $ より,これをみたす $ \theta $ は,
$ \dfrac{\pi}{2}< \theta< \pi $ ,
$ \dfrac{3\pi}{2}<\theta<2\pi $ に1個ずつある。
それを $ \theta_1 $ , $ \theta_2 $ とする。
$ \dfrac{\pi}{2}< \theta< \pi $ のとき, $ \sin\theta $ の $ \cos\theta $ も減少するので,
$ f'(\theta) $ は $ \theta_1 $ で正からに負に変わり, $ \theta_1 $ で極大,
$ \dfrac{3\pi}{2}< \theta< 2\pi $ のとき, $ \sin\theta $ の $ \cos\theta $ も増加するので,
$ f'(\theta) $ は $ \theta_2 $ で負から正に変わり,この $ \theta_2 $ で極小である。
したがって, $ a^2-b^2=f(\theta) $ が異なる4つの解をもつのは
\[
a^2-b^2>f(\theta_2)
\]
のときである。
$ \tan\theta_2=-\left(\dfrac{bY}{aX} \right)^{\frac{1}{3}} $ より,
\[
\cos^2\theta_2=\dfrac{(aX)^{\frac{2}{3}}}{(aX)^{\frac{2}{3}}+(bY)^{\frac{2}{3}}},\ \quad
\sin^2\theta_2=\dfrac{(bY)^{\frac{2}{3}}}{(aX)^{\frac{2}{3}}+(bY)^{\frac{2}{3}}}
\]
ここで, $ \cos\theta_2 >0 $ , $ \sin\theta_2< 0 $ なので,
\[
\cos\theta_2=\dfrac{(aX)^{\frac{1}{3}}}{\sqrt{(aX)^{\frac{2}{3}}+(bY)^{\frac{2}{3}}}},\ \quad
\sin\theta_2=\dfrac{-(bY)^{\frac{1}{3}}}{\sqrt{(aX)^{\frac{2}{3}}+(bY)^{\frac{2}{3}}}}
\]
となる.よって,
\begin{eqnarray*}
f(\theta_2)&=&
\dfrac{aX\sqrt{(aX)^{\frac{2}{3}}+(bY)^{\frac{2}{3}}}}{(aX)^{\frac{1}{3}}}-
\dfrac{bY\sqrt{(aX)^{\frac{2}{3}}+(bY)^{\frac{2}{3}}}}{-(bY)^{\frac{1}{3}}}\\
&=&\{(aX)^{\frac{2}{3}}+(bY)^{\frac{2}{3}}\}\sqrt{(aX)^{\frac{2}{3}}+(bY)^{\frac{2}{3}}}\\
&=&\{(aX)^{\frac{2}{3}}+(bY)^{\frac{2}{3}}\}^{\frac{3}{2}}\\
&<&a^2-b^2
\end{eqnarray*}
これより,
\[
(ax)^{\frac{2}{3}}+(by)^{\frac{2}{3}}<(a^2-b^2)^{\frac{2}{3}}
\quad \cdots③
\]
となることが示された.
$ X $ , $ Y $ のいずれかが負であるときも,図形の対称性と不等式の対称性から,
同様の関係が成り立つ。
$ X>0 $ , $ Y=0 $ のとき
平行条件 $ ② $ は
\[
\dfrac{\cos\theta}{a}\left(b\sin\theta \right)-
\dfrac{\sin\theta}{b}\left(a\cos\theta-X \right)=0
\]
となり, $ \theta=0,\ \pi $ のとき成立し,
さらに $ \theta\ne 0,\ \pi $ のときは
\[
\cos\theta=\dfrac{aX}{a^2-b^2}
\]
となる。さらに,この $ \theta $ が2個とれるのは,
$ \left|\dfrac{aX}{a^2-b^2} \right|<1 $ のときで,
このとき条件は
$ ③ $ と同値である。
$ X=0 $ , $ Y >0 $ のときも同様である。
$ X=Y=0 $ なら法線は $ x $ 軸と $ y $ 軸にとれ,対応する点は4個ある。 $ X=Y=0 $ は $ ③ $ をみたす。
以上から,平面上の点 $ \mathrm{P} $ から少なくとも4本の異なる法線が引ける条件が,
$ ③ $ であることが示された。