一橋後期5番解答
[I]
$ x< -1 $ のとき. $ \displaystyle \lim_{m \to \infty}x^{2m+1}=-\infty $ なので,
任意の実数 $ y $ に対して $ x^n< y $ となる $ n $ が存在する.
$ -1\leqq x< 0 $ のとき.
$ x^1< x^3< \cdots< 0< x^{2m} $ なので, $ x< y $ であるときにかぎり $ n=1 $ が条件を満たす.
$ x=0 $ のとき. $ 0< y $ が条件である.
$ 0< x< 1 $ のとき.
$ \displaystyle \lim_{n \to \infty}x^n=0 $ なので,
$ 0< y $ であるとき, $ 0< x^n< y $ となる $ n $ が存在する.
$ 1\leqq x $ のとき. $ x^1< x^2< \cdots $ なので, $ x^1=x< y $ の $ y $ が条件を満たす.
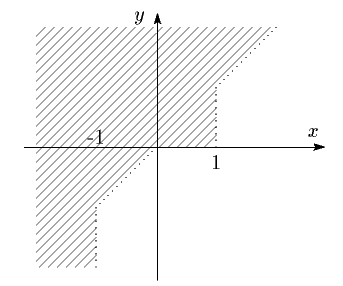
以上より,条件を満たす点 $ (x,\ y) $ 全体の集合は次図のようになる.
ただし境界は含まない.
[II]
部分積分により,
\begin{eqnarray*}
\int_0^xe^{-t}f(x-t)\,dt &=&
\left[-e^{-t}f(x-t) \right]_0^x-\int_0^x(-e^{-t})\{-f'(x-t)\}\,dt\\
&=&f(x)-\int_0^xe^{-t}f'(x-t)\,dt
\end{eqnarray*}
これより,
\[
f(x)-\int_0^xe^{-t}f(x-t)\,dt=\int_0^xe^{-t}f'(x-t)\,dt
\quad \cdots①
\]
一方, $ x-t=s $ とおくと,
\[
\int_0^xe^{-t}f(x-t)\,dt=\int_x^0e^{-x+s}f(s)\,(-ds)
=e^{-x}\int_0^xe^sf(s)\,ds
\]
であるから,
\begin{eqnarray*}
\dfrac{d}{dx}\left(\int_0^xe^{-t}f(x-t)\,dt \right)&=&\dfrac{d}{dx}\left(e^{-x}\int_0^xe^sf(s)\,ds\right)\\
&=&-e^{-x}\int_0^xe^sf(s)\,ds+e^{-x}\cdot e^xf(x)\\
&=&f(x)-e^{-x}\int_0^xe^sf(s)\,ds\\
&=&f(x)-\int_0^xe^{-t}f(x-t)\,dt
\end{eqnarray*}
したがって $ ① $ より,
\[
\dfrac{d}{dx}\left(\int_0^xe^{-t}f(x-t)\,dt \right)=
\int_0^xe^{-t}f'(x-t)\,dt
\]
が示された.