特色入試総人理系1番解答
(1) 平面上の2つの円は相似である。 三角形△PQRの外接円を $ C $ とすると $ C $ と $ \gamma $ は相似である。 $ C $ 上の3点 P,Q,R に対応する $ \gamma $ 上の3点を A,B,Cとすると △PQR ∽ △ABC となる。
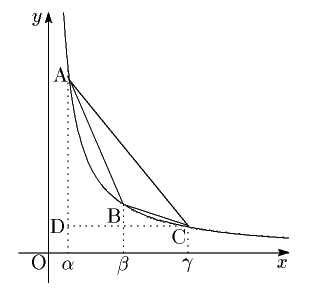
(2) $ \gamma $ 上の3点を A $ \left(\alpha,\ \dfrac{1}{\alpha} \right) $ , B $ \left(\beta,\ \dfrac{1}{\beta} \right) $ , C $ \left(\gamma,\ \dfrac{1}{\gamma} \right) $ $ (\alpha<\beta<\gamma) $ とする。 点D $ \left(\alpha,\ \dfrac{1}{\gamma} \right) $ をとる。 $ \dfrac{1}{\alpha}<\dfrac{1}{\gamma} $ なので,点Dは第1象限の $ y<\dfrac{1}{x} $ で定まる領域にある。 \[ \angle \mathrm{CAB}<\angle \mathrm{CAD},\ \quad \angle \mathrm{ACB}<\angle \mathrm{ACD} \] で, $ \angle \mathrm{ADC}=\dfrac{\pi}{2} $ なので, $ \bigtriangleup \mathrm{ABC} $ はつねに鈍角三角形となる。 よって,鋭角三角形△PQRに対しては,△PQR ∽ △ABC となる3点A,B,C の組は存在しない。
(3) 鈍角三角形△PQR に対して △PQR ∽ △ABC となる3点A,B,C の組は, 点Aと点Bを $ y=\dfrac{1}{x} $ 上に任意にとれば,それに対してCは一意に定まる。 点Aと点Bが $ y=\dfrac{1}{x} $ 上を連続して動けば,点Cも連続して動く。 最初△ABCは△A $ _1 $ B $ _1 $ C $ _1 $ であるとする。 A $ _1 $ とB $ _1 $ を,その $ x $ 座標を十分小さくとり, 直線B $ _1 $ C $ _1 $ の $ x $ 軸に対する傾きが負であり, 点C $ _1 $ が領域 $ y>\dfrac{1}{x} $ にあるようにとる。鈍角三角形なので,可能である。 辺ABの長さをのばしてゆき,図の△A $ _2 $ B $ _2 $ C $ _2 $ 間で連続的に変化させるとする。 ただし,△A $ _2 $ B $ _2 $ C $ _2 $ の頂点C $ _2 $ は領域 $ y<\dfrac{1}{x} $ にあるものとする。 これもまた可能である。
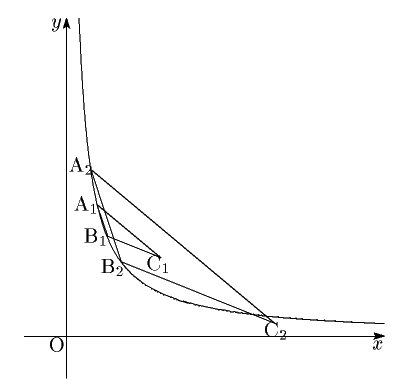
△ABCを△A $ _1 $ B $ _1 $ C $ _1 $ から△A $ _2 $ B $ _2 $ C $ _2 $ 間で連続的に変化させるとき,
点Cの動きも連続的なので,点Cが $ y=\dfrac{1}{x} $ 上にあるときがある。
このとき,△ABCは $ \gamma $ 上にある。
つまり,△PQR ∽ △ABC となる3点A,B,Cが $ \gamma $ 上に存在することが示された。