また,3直線が平行な場合も1点で交わる場合も同じように考えることができることを,線束の概念でくくることで示している.このような幾何を実際に見出すことは今後の課題である.それはおさえたうえで,この立場から考える例は,六角形の頂点が一般の位置にある,つまり2頂点を結ぶ直線はいずれも平行でないとしてよい.
このような場合についていろいろな例を作ることが大切である.そこで,円周上に左回りに6点A,B,C,D,E,F があるとしよう.パスカルの定理によって,
まずパスカル線は何本あるか.記号
![]() で,上下の入れかえと
で,上下の入れかえと
![]() ,
,
![]() ,
,
![]() の並べ替えは同じ3交点になるので,パスカル線は
の並べ替えは同じ3交点になるので,パスカル線は
いちどはこれをすべて描いてみたいものだ.その上で次のサイトには,点を動かしたときのパスカル線の変化を実際に見ることができる.制作者に感謝して紹介する.
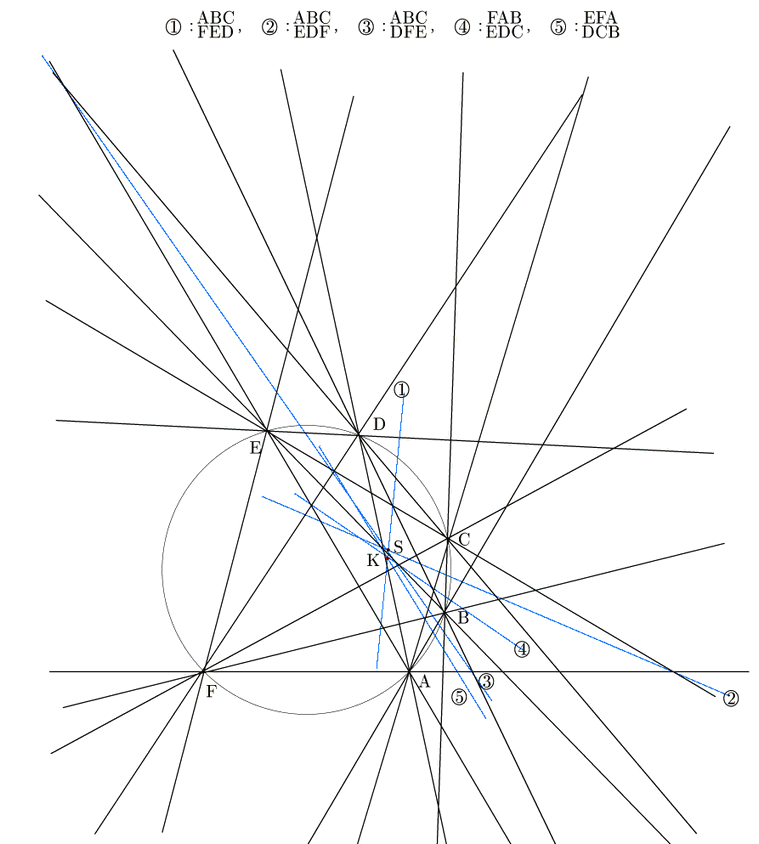
これから見えてくることは,3本のパスカル線![]() ,
,![]() ,
,![]() は共線ではないか,また3本のパスカル線
は共線ではないか,また3本のパスカル線![]() ,
,![]() ,
,![]() も共点ではないかということである.実はこれが成りたつ.
も共点ではないかということである.実はこれが成りたつ.
これらについては,ウエブサイト Pascal Lines: Steiner and Kirkman Theorems で実験できる.またその証明は参考文献『幾何学大辞典6』の「附録」にある.ここには,その他のさらなる相互関係も紹介されている.これらはパスカルの論文からおよそ二百年後,十九世紀中葉に大いに研究され,ほぼそのすべてが解明されたのである.これらがパスカルの定理からその応用として導かれる.
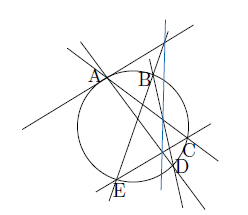 六角形の頂点AとBを結び,その上で点Bを点Aに近づけると,直線ABは点Aでの接線になる.これは接線の定義そのものである.
六角形の頂点AとBを結び,その上で点Bを点Aに近づけると,直線ABは点Aでの接線になる.これは接線の定義そのものである.
このような連続的な変化に対して,点BがAにいくら近づいても異なる点であるかぎりパスカル線は存在するので,点Bを点Aに近づけるとパスカル線も動くが,接線になったときも3交点は共線である.これを同様に
![]() と記す.これは円周上に5点A,B,C,D,Eをとり,AAを結ぶときは点Aでの接線をとるものとすることを意味する.
と記す.これは円周上に5点A,B,C,D,Eをとり,AAを結ぶときは点Aでの接線をとるものとすることを意味する.
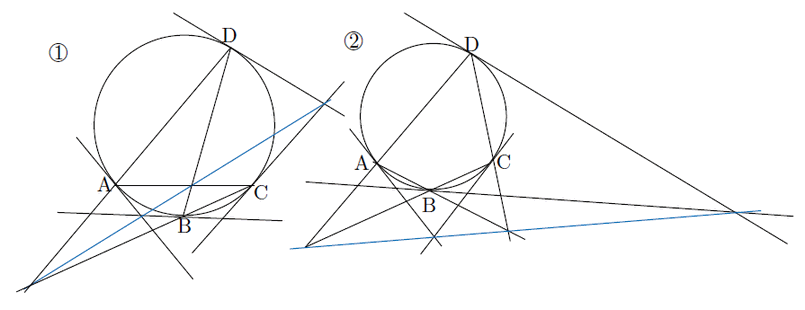
次に,円周上に4点A,B,C,Dがあり,そのうち2本を接線とする場合を考える.次のようにパスカル線が一致する場合などが起こる.この場合パスカル線は何本あるか.4点のうちどの2点で接線を引くかは
![]() 通り.例えばそれをAとBとする.CとDの使い方は次の3通りである.
通り.例えばそれをAとBとする.CとDの使い方は次の3通りである.
このうち,
![]() と
と
![]() の2本のパスカル線は2点
の2本のパスカル線は2点
![]() と
と
![]() を共有し,したがって一致する(下図
を共有し,したがって一致する(下図![]() ).
).
もう一例.
![]() と
と
![]() の2本のパスカル線は2点
の2本のパスカル線は2点
![]() と
と
![]() を共有し,したがって一致する.(下図
を共有し,したがって一致する.(下図![]() )このように一致するパスカル線が2本ずつあり,合計6本のパスカル線は2本ずつ重なって3本になる.
)このように一致するパスカル線が2本ずつあり,合計6本のパスカル線は2本ずつ重なって3本になる.
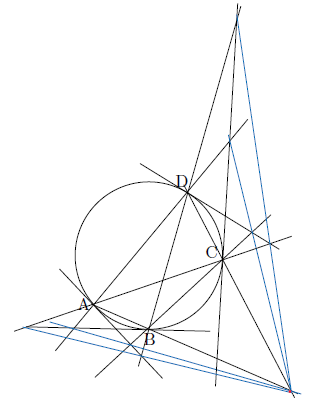 一方,
一方,
あわせて18本あり,これが2点で接線を引く場合である.
3点A,B,Cにおいて3接線を引く場合は,パスカル線は
![]() の1本しかない.
の1本しかない.
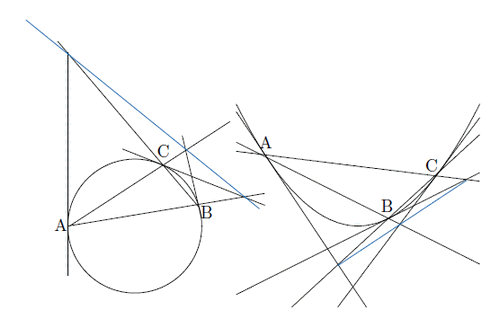
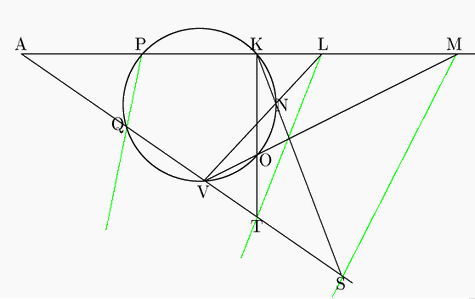
自分でいろいろな図を書いてその神秘さにふれることを心から勧める.