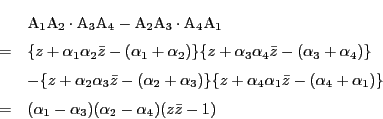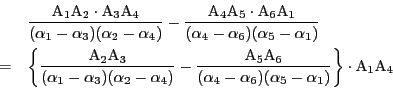次: 重心座標の方法
上: 証明の試み
前: 複比という方法
次: 重心座標の方法
上: 証明の試み
前: 複比という方法
命題1を座標幾何で示すことはできないか.円を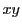 座標平面に置き,直線の方程式を考えることにより証明することを試みよう.円周上の点を角と三角関数で表すことで考えるのであるが,やってみれば式がたいへん複雑になる.円周上の点,およびそれらを通る直線を表すより簡明な方法がある.それが複素平面の方法である.この方法は本質的には座標の方法であるが,複素数を用いることでその記述が簡明になるのである.座標方程式に直そうとすればできなくはないが,実際にやってみるとたいへん複雑になる.
座標平面に置き,直線の方程式を考えることにより証明することを試みよう.円周上の点を角と三角関数で表すことで考えるのであるが,やってみれば式がたいへん複雑になる.円周上の点,およびそれらを通る直線を表すより簡明な方法がある.それが複素平面の方法である.この方法は本質的には座標の方法であるが,複素数を用いることでその記述が簡明になるのである.座標方程式に直そうとすればできなくはないが,実際にやってみるとたいへん複雑になる.
複素数 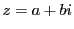 に対して
に対して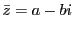 を共役複素数,また負でない実数
を共役複素数,また負でない実数
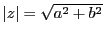 を
を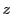 の絶対値という.定義から
の絶対値という.定義から
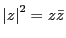 である.また,
である.また,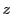 が実数であることと
が実数であることと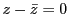 が同値,
が同値,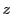 が純虚数であることと
が純虚数であることと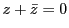 が同値である.
が同値である.
さて,複素数 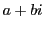 に直交座標平面の点
に直交座標平面の点 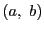 を対応させることにより,実数の集合が数直線になるように,複素数の集合
を対応させることにより,実数の集合が数直線になるように,複素数の集合 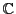 は複素平面になる.複素平面のうち実数に対応する部分を実軸,純虚数に対応する部分と0を虚軸という.これによって,平面図形を複素数で考えることができるようになる.
は複素平面になる.複素平面のうち実数に対応する部分を実軸,純虚数に対応する部分と0を虚軸という.これによって,平面図形を複素数で考えることができるようになる.
複素数は極形式という表し方がある.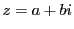 のとき,
のとき,
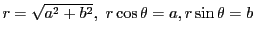 となる
となる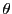 がとれる.これによって
がとれる.これによって
となる.複素数のこの形での表示が極形式である.角 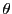 は
は 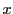 軸の正の方向から反時計回りにとる.角
軸の正の方向から反時計回りにとる.角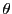 は複素数
は複素数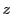 の偏角とよばれ
の偏角とよばれ 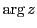 と書く.
と書く.
「形式」というのは「形」でのことで,同じ複素数 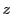 が,
が,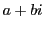 と
と
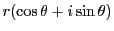 という二つの形をもつ.二つの複素数
という二つの形をもつ.二つの複素数
をとる.三角関数の加法定理によって
となり,同様にして
となる.これから複素数の偏角は
をみたし,あたかも対数関数のような形になる.
補題 8 (
ド・モアブルの定理)
任意の整数

に対して
が成り立つ.■
証明
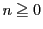 のとき.数学的帰納法で示す.
のとき.数学的帰納法で示す.
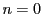 のときは両辺1であるから成立する.
のときは両辺1であるから成立する.
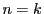 で成立するとして,
で成立するとして,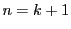 で成立することを示す.
で成立することを示す.
よって, が負でないときは示された.
が負でないときは示された.
次に, 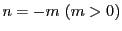 のとき
のとき
よって, この場合も成立し,題意は示された.
□
直交座標平面で直線の表し方は二つあった.
一つは2点 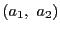 と
と 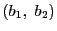 を通る直線は
を通る直線は
となる.
もう一つは,点 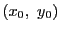 を通りベクトル
を通りベクトル 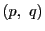 に垂直な直線は
に垂直な直線は
となる.
それと同じように,複素数による直線の表し方も二通りある.
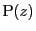 を動点とし,
を動点とし,
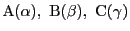 などを
定点とする.また
などを
定点とする.また 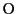 は原点である.
は原点である.
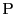 が次の図形上にあるとき,
が次の図形上にあるとき, 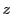 の満たすべき式を
の満たすべき式を
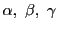 などの複素数の(共役,絶対値などを用いた)等式で表わそう.
などの複素数の(共役,絶対値などを用いた)等式で表わそう.
まず第一の型での表現.
- (1)
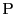 が
が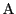 を通り直線
を通り直線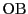 と平行な直線上にあることを,複素数で表す.
と平行な直線上にあることを,複素数で表す.
条件から,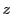 は実数
は実数 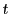 を用いて
を用いて
と表される.つまり
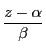 が実数である.
これを等式として表すと次のようになる.
が実数である.
これを等式として表すと次のようになる.
- (2)
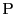 が直線
が直線 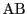 上の点であることを複素数で表す.
上の点であることを複素数で表す.
直線 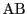 上の点は
上の点は 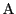 を通りABに平行な直線であるから(1)から
を通りABに平行な直線であるから(1)から
つまり
次は第二の型での表現.
- (1)
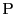 が,
定点
が,
定点 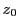 を通り直線
を通り直線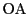 と直交する直線上にあることを複素数で表す.
と直交する直線上にあることを複素数で表す.
これは
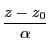 が純虚数と同値なので.
が純虚数と同値なので.
- (2)
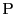 が線分
が線分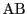 の垂直二等分線上にあることを複素数で表す.
の垂直二等分線上にあることを複素数で表す.
線分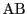 の垂直二等分線上の点はAとBからの距離が等しいことと同値である.
の垂直二等分線上の点はAとBからの距離が等しいことと同値である.
第一の型は両辺が純虚数で,これを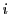 で割って係数を置きなおすと第二の型になる.
一般に
で割って係数を置きなおすと第二の型になる.
一般に
という形をした式は, 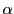 と直交する直線を表す.なぜならこの式を満たす任意の一点
と直交する直線を表す.なぜならこの式を満たす任意の一点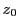 をとる.
をとる.
二式の辺々を引く.
つまり
となるので,
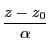 が純虚数.ゆえに,条件式を満たす
が純虚数.ゆえに,条件式を満たす 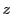 の集合は
の集合は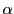 と直交する直線になる.
と直交する直線になる.
以上の準備のもとに,命題1を,いずれの2点を結ぶ直線も互いに交点をもつものとする.つまり平行とならない一般的な位置にあるものとして証明しよう.
証明
円の半径は1であるとしてよい.
6点
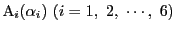 が原点
が原点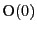 を中心とする半径1の円周上にあるとする.
を中心とする半径1の円周上にあるとする.
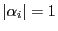 であり,
であり,
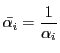 である.
である.
直線
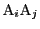 の方程式は
の方程式は
である.記号
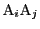 でこの直線の方程式も表す.この方程式を分母を払い
でこの直線の方程式も表す.この方程式を分母を払い
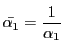 等を用いて整理すると
等を用いて整理すると
となる.さて二つの直線の方程式の左辺の積
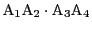 は2次式である.そこで方程式
は2次式である.そこで方程式
を考える.
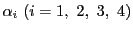 はこの方程式を満たす.左辺は二次である.従ってもし可約でなければ円の方程式と一致するはずである.実際にこれを計算してみる.
はこの方程式を満たす.左辺は二次である.従ってもし可約でなければ円の方程式と一致するはずである.実際にこれを計算してみる.
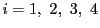 に代えて
に代えて
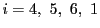 をとっても同様になる.この結果
をとっても同様になる.この結果
を得る.これから
を得る.この等式の左辺を2点
は満たす.
しかしこれらの点は直線
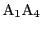 上にはない.
よってこれら2点は方程式
上にはない.
よってこれら2点は方程式
で定まる直線上にある.点
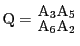 もこの上にあるので,これら3点は共線である.
□
もこの上にあるので,これら3点は共線である.
□
パスカルの補題Iという名の基本定理はいくつかの初等的方法で示された.もちろんそこにある方法の不統一や,平行な場合に場合分けしなければならない等の問題が残った.一方,6点の配列順にはよらない方法は,複比を用いる方法と複素平面上に置く方法で得られた.これらのことは逆にユークリッド幾何がむしろ特別な一幾何であってより包括的で普遍的な幾何がその背後にあるのではないかということを,われわれに示唆している.その幾何を発見しよう.


 次: 重心座標の方法
上: 証明の試み
前: 複比という方法
2014-01-03
次: 重心座標の方法
上: 証明の試み
前: 複比という方法
2014-01-03
![]() に対して
に対して![]() を共役複素数,また負でない実数
を共役複素数,また負でない実数
![]() を
を![]() の絶対値という.定義から
の絶対値という.定義から
![]() である.また,
である.また,![]() が実数であることと
が実数であることと![]() が同値,
が同値,![]() が純虚数であることと
が純虚数であることと![]() が同値である.
が同値である.
![]() に直交座標平面の点
に直交座標平面の点 ![]() を対応させることにより,実数の集合が数直線になるように,複素数の集合
を対応させることにより,実数の集合が数直線になるように,複素数の集合 ![]() は複素平面になる.複素平面のうち実数に対応する部分を実軸,純虚数に対応する部分と0を虚軸という.これによって,平面図形を複素数で考えることができるようになる.
は複素平面になる.複素平面のうち実数に対応する部分を実軸,純虚数に対応する部分と0を虚軸という.これによって,平面図形を複素数で考えることができるようになる.
![]() が,
が,![]() と
と
![]() という二つの形をもつ.二つの複素数
という二つの形をもつ.二つの複素数
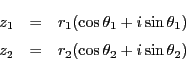
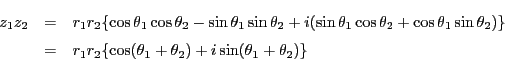
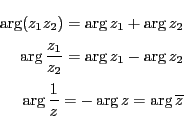
![]() のときは両辺1であるから成立する.
のときは両辺1であるから成立する.
![]() で成立するとして,
で成立するとして,![]() で成立することを示す.
で成立することを示す.
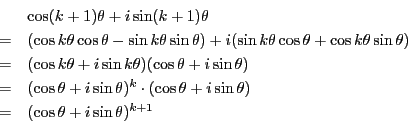
![]() のとき
のとき
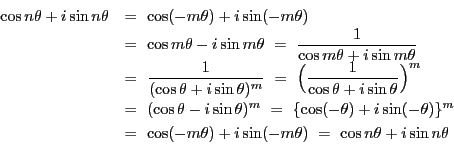
![]() と
と ![]() を通る直線は
を通る直線は
![]() を動点とし,
を動点とし,
![]() などを
定点とする.また
などを
定点とする.また ![]() は原点である.
は原点である.
![]() が次の図形上にあるとき,
が次の図形上にあるとき, ![]() の満たすべき式を
の満たすべき式を
![]() などの複素数の(共役,絶対値などを用いた)等式で表わそう.
などの複素数の(共役,絶対値などを用いた)等式で表わそう.
![]() は実数
は実数 ![]() を用いて
を用いて
![]() 上の点は
上の点は ![]() を通りABに平行な直線であるから(1)から
を通りABに平行な直線であるから(1)から
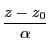 が純虚数と同値なので.
が純虚数と同値なので.
![]() の垂直二等分線上の点はAとBからの距離が等しいことと同値である.
の垂直二等分線上の点はAとBからの距離が等しいことと同値である.
![]() で割って係数を置きなおすと第二の型になる.
一般に
で割って係数を置きなおすと第二の型になる.
一般に
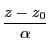 が純虚数.ゆえに,条件式を満たす
が純虚数.ゆえに,条件式を満たす ![]() が原点
が原点![]() を中心とする半径1の円周上にあるとする.
を中心とする半径1の円周上にあるとする.
![]() であり,
であり,
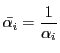 である.
である.
![]() の方程式は
の方程式は
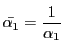 等を用いて整理すると
等を用いて整理すると