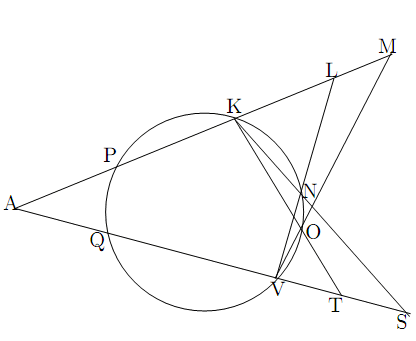
 命題 7
円の外部の点Aから円に交わる2直線を引き,交点をP,KとQ,Vとする.さらに円周上の2点O,Nをとり,KO,KNと直線AQの交点をT,S,またVN,VOと直線APの交点をL,Mとする.このとき等式
命題 7
円の外部の点Aから円に交わる2直線を引き,交点をP,KとQ,Vとする.さらに円周上の2点O,Nをとり,KO,KNと直線AQの交点をT,S,またVN,VOと直線APの交点をL,Mとする.このとき等式
また,命題のうちには,円の場合に示すことが補題IIによって円錐曲線でも成立するものと,円錐曲線への一般化を吟味しなければならないものがある.円の場合で考えながら,一般化への課題も考える.また,命題5はユークリッド平面内の有心円錐曲線で考えることにしよう.用いる方法は複比の方法である.また,パスカルはギリシア以来の合成比を用いて表現している.その命題群を今風に言い直して円の場合に再掲する.また線分は有向線分として考えることにする.
 命題 7
円の外部の点Aから円に交わる2直線を引き,交点をP,KとQ,Vとする.さらに円周上の2点O,Nをとり,KO,KNと直線AQの交点をT,S,またVN,VOと直線APの交点をL,Mとする.このとき等式
命題 7
円の外部の点Aから円に交わる2直線を引き,交点をP,KとQ,Vとする.さらに円周上の2点O,Nをとり,KO,KNと直線AQの交点をT,S,またVN,VOと直線APの交点をL,Mとする.このとき等式
証明 証明すべき等式は
証明
第一の等式は
次に命題IIの後半である.その内容を円の場合に示す.
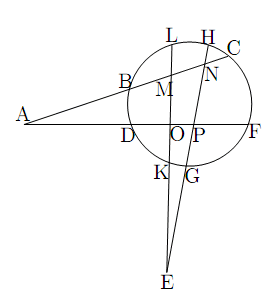
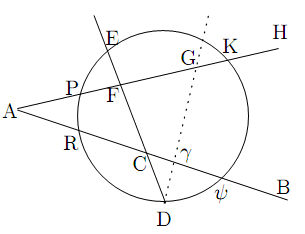 命題 9
点E,Dを通る一つの円が直線AH,ABを点P,K,R,
命題 9
点E,Dを通る一つの円が直線AH,ABを点P,K,R,![]() で切るならば,
で切るならば,
証明
命題8より
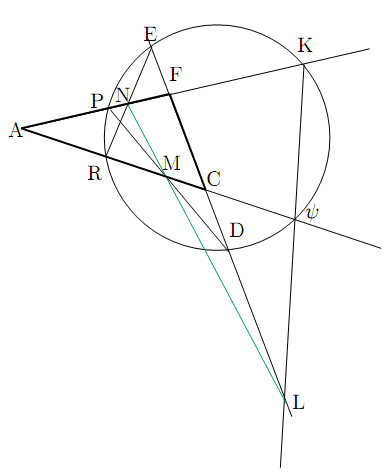 六角形
六角形
![]() においてパスカル線
においてパスカル線
![]() を引く.交点を図のように順にL,M,Nとする.
を引く.交点を図のように順にL,M,Nとする.
![]() と,
直線L
と,
直線L![]() K,直線DMP,直線NRE,および直線LMNに関してメネラウスの定理を用いる.
K,直線DMP,直線NRE,および直線LMNに関してメネラウスの定理を用いる.

実は円の場合,方べきの定理
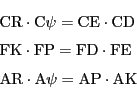
 命題 10
4直線AC,AF,EH,ELが点N,P,M,Oで交わり,一つの円がこれらの直線を点C,B,F,D,H,G,L,Kで切るなら,
命題 10
4直線AC,AF,EH,ELが点N,P,M,Oで交わり,一つの円がこれらの直線を点C,B,F,D,H,G,L,Kで切るなら,
証明
命題9の証明で得られた等式は点
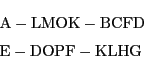

本命題も円の場合は方べきの定理からただちに得られる.しかし,カルノーの方法にもとづくこの証明でないと一般の円錐曲線の場合に耐えられない.
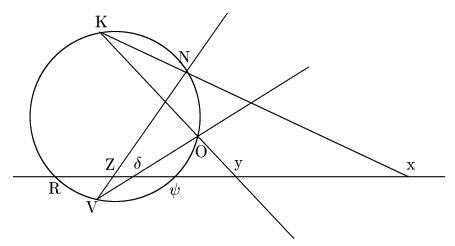 命題 11
4点K,N,O,Vを通る円錐曲線を直線R
命題 11
4点K,N,O,Vを通る円錐曲線を直線R![]() で切る.KN,KOとの交点をx,yとし,
VN,VOとの交点をZ,
で切る.KN,KOとの交点をx,yとし,
VN,VOとの交点をZ,![]() とすれば
とすれば
証明
本等式は
後に射影直線の射影変換を定義する.
射影変換は複比を変えない.
4点
![]() を
を
![]() に変換する射影変換は,
もういちどおこなうと
に変換する射影変換は,
もういちどおこなうと
![]() を固定し,恒等変換になる.
このように二回くりかえすと恒等変換になる射影変換を対合といい,
対合で対応する点も対合という.つまり
この命題は円錐曲線を直線で切って得られる点の組
を固定し,恒等変換になる.
このように二回くりかえすと恒等変換になる射影変換を対合といい,
対合で対応する点も対合という.つまり
この命題は円錐曲線を直線で切って得られる点の組
対合を発見したのはデザルグである.
一直線上に点Oが存在し,
となるようにできるとき,点列
は対合をなすという.
これがデザルグの発見した概念である.デザルグはこの概念の下,1639年,円錐曲線に内接する四辺形を一直線で切って得られる6点は対合をなすことを発見,この証明の形で証明した.
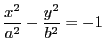 となる共役双曲線をあわせて考える.
となる共役双曲線をあわせて考える.
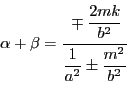
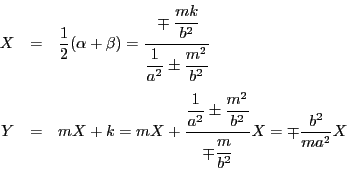
直径![]() が円錐曲線と交わる点を
が円錐曲線と交わる点を![]() とすると,
とすると,![]() であって,交点での接線は
であって,交点での接線は
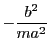 である.
である.
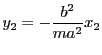 である.
である.
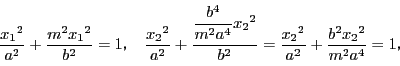
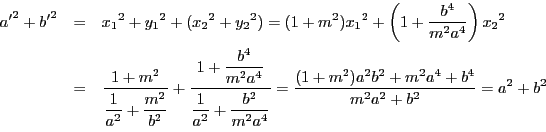
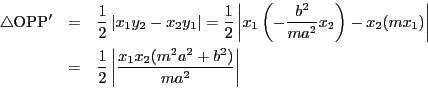
点![]() の媒介変数表示が
の媒介変数表示が
![]() であるとき,
点
であるとき,
点![]() の媒介変数表示は
の媒介変数表示は
双曲線の場合は![]() は共役双曲線上に現れる.
は共役双曲線上に現れる.
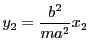 である.
である.
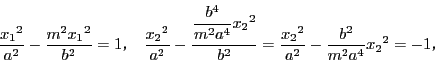
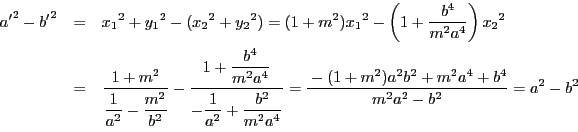
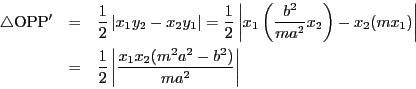
証明 記号はこれまでと同様にとる.
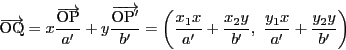
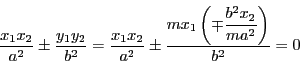
そのうえで,命題Vでパスカルが言いたかったと思われることを命題とする.
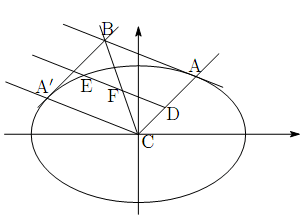 命題 12
平面上にCを中心とする双曲線,楕円あるいは円がある.直線ABが点Aでこの円錐曲線に接している.A
命題 12
平面上にCを中心とする双曲線,楕円あるいは円がある.直線ABが点Aでこの円錐曲線に接している.A![]() をCA
をCA![]() がCAに対する共役直径になる円錐曲線上の点とする.直径CAを引き,直線ABをCA
がCAに対する共役直径になる円錐曲線上の点とする.直径CAを引き,直線ABをCA![]() に等しくとる.またCBを引く.直線ABに平行な任意の直線DEを引く.円錐曲線をEで,直線AC,CBを点D,Fで切る.円錐曲線が楕円あるいは円なら,直線DE,DFの平方の和は直線ABの平方の和に等しい.双曲線の場合には,同じ直線DE,DFの平方の差が直線ABの平方に等しい.
■
に等しくとる.またCBを引く.直線ABに平行な任意の直線DEを引く.円錐曲線をEで,直線AC,CBを点D,Fで切る.円錐曲線が楕円あるいは円なら,直線DE,DFの平方の和は直線ABの平方の和に等しい.双曲線の場合には,同じ直線DE,DFの平方の差が直線ABの平方に等しい.
■
証明
記号など補題を踏襲する.
楕円の場合で示す.
すると
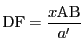 である.
である.