

 次: 確率は賭け事の理論
上: 確率論の始まり
前: 確率論の始まり
次: 確率は賭け事の理論
上: 確率論の始まり
前: 確率論の始まり
確率とは何か.その基本が分からなければいつまでも苦手である.
また,確率問題では,事象の確率をどのように定めるのか,
あるいは「何が同様に確からしいのか」を定めるのか,それが指示されず,
そこを常識の範囲で考えなければならないこともあり,
そこにも難しさがある.次の例を考えよう.
例 1
区別のつかない硬貨を2枚同時に投げる.
2枚の表裏が一致する確率を求めよ.
- 解答
- 硬貨が区別されないので
試行の結果は(表,表),(表,裏),(裏,裏)の3通りある.
このうち2枚の表裏が一致する場合は2通り.
よって求める確率は
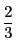 .
.
この解答は正しくない.
では,なぜ正しくないのか,指摘できるだろうか.
上の例の計算では,
該当する出方の総数を,すべての出方の場合の数で割っている.
つまり,
「区別がないのだから(表,表),(表,裏),(裏,裏)の3通りは起こる確率は等しい」と
勝手にしている.
1枚の硬貨が表であるか裏であるかが同様に確かで,各確率は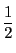 である.
よって1枚目の硬貨が表裏か,2枚目の硬貨が表裏かを区別しなければならない.
である.
よって1枚目の硬貨が表裏か,2枚目の硬貨が表裏かを区別しなければならない.
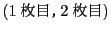 の出方は
の出方は
の4通りある.これらが同様に確かとなる.
このうち2枚の表裏が一致する場合は2通り.
よって求める確率は 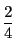 としなければならない.
としなければならない.
(表,表),(表,裏),(裏,表),(裏,裏)の4通りが同様に確かである根拠は何か.
それは
- 1枚の硬貨を投げたときに,表がでるか裏がでるかが同様に確からしい.
- 2枚の硬貨を投げる試行で,
各々の硬貨についての事象は互いに影響しない.
ということである.
つまり1枚の硬貨について表が出る確率,裏が出る確率がそれぞれ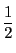 .
1枚目が表であれ,裏であれ,2枚目が表になるか裏になるかは,同様に確かである.
すると2枚の硬貨を投げるなら,
それぞれの硬貨の表裏の組合せ,
「(表,表),(表,裏),(裏,表),(裏,裏)」の4通りが同様に確からしい.
事象の総数が4であるから,各確率はそれぞれ
.
1枚目が表であれ,裏であれ,2枚目が表になるか裏になるかは,同様に確かである.
すると2枚の硬貨を投げるなら,
それぞれの硬貨の表裏の組合せ,
「(表,表),(表,裏),(裏,表),(裏,裏)」の4通りが同様に確からしい.
事象の総数が4であるから,各確率はそれぞれ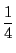 である.
ここまで考えれば,納得がいく.
である.
ここまで考えれば,納得がいく.
この方面で間違いやすい問題を紹介する.次の問題の(4)を注意して解いてみよう.
問題 1
[2000年長崎総合科学大学]
解答
1
12人の人がボールを1個ずつ持っていて,順番に A,B,C の箱のいずれかに入れていく
ものとする.このとき,次の各問いに答えよ.ただし,同名の人はなく,空の箱が
あってもよいものとする.
- ボールに自分の名前を書いて箱に入れていく場合,ボールの入り方は
何通りあるか.
- ボールに自分の名前を書いて箱に入れていく場合,A にちょうど8個の
ボールが入る入り方は何通りあるか.
- ボールに名前を書かずに箱に入れていく場合,A,B,C の箱に入った
ボールの個数の組み合わせは何通りあるか.
- ボールに名前を書かずに箱に入れていく場合,8個以上のボールが入る
箱がある確率を求めよ.
Aozora
2017-09-13
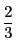 .
.
![]() である.
よって1枚目の硬貨が表裏か,2枚目の硬貨が表裏かを区別しなければならない.
である.
よって1枚目の硬貨が表裏か,2枚目の硬貨が表裏かを区別しなければならない.
![]() の出方は
の出方は