

 次: ユークリッドの互除法
上: 約数と倍数
前: 約数と倍数
次: ユークリッドの互除法
上: 約数と倍数
前: 約数と倍数
定義 2
整数

が
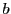
の
倍数であるとは,
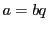
となる整数
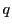
が存在することと定める.
このとき
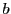
は

の
約数という.
除法の定理によって,

が
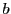
の倍数であることは,

を
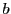
で割った余りが0であることと同値である.■
さらに,公約数,公倍数が定義される.
定義 3
二つ以上の整数
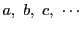
に共通な倍数をそれらの整数の公倍数という.
0は常に公倍数である.
それを除けば公倍数の絶対値は
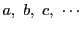
のいずれの絶対値よりも小さくはないので,
公倍数の中に正で最小のものがある.
それを
最小公倍数(least common multiple 略して L.C.M.)という.
二つ以上の整数
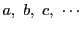 に共通な約数をそれらの整数の公約数という.
1は常に公約数である.
公約数の絶対値は
に共通な約数をそれらの整数の公約数という.
1は常に公約数である.
公約数の絶対値は
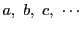 のいずれの絶対値よりも大きくはないので,
公約数の中に最大のものがある.
それを最大公約数(greatest common measure 略して G.C.M.)という.■
のいずれの絶対値よりも大きくはないので,
公約数の中に最大のものがある.
それを最大公約数(greatest common measure 略して G.C.M.)という.■
最大公約数が1であるとき,その2数は互いに素であるという.
また整数 と
と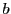 の最大公約数を座標などと混同する恐れのないときは
の最大公約数を座標などと混同する恐れのないときは
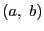 と書く.
と書く.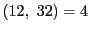 のように用いる.
のように用いる.
定理 2
- (1)
- 二つ以上の整数の公倍数は,最小公倍数の倍数である.
- (2)
- 二つ以上の整数の公約数は,最大公約数の約数である.
- (3)
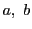 の最小公倍数を
の最小公倍数を 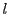 ,最大公約数を
,最大公約数を 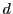 とすれば
とすれば 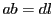 .
.
- (4)
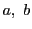 が互いに素で,他の整数
が互いに素で,他の整数 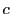 と
と 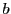 との積
との積 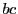 が
が  で
割りきれるなら,実は
で
割りきれるなら,実は 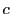 が
が  で割りきれる.■
で割りきれる.■
証明
(1)
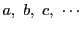 の最小公倍数を
の最小公倍数を 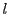 とし,
とし, 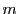 を任意の公倍数とする.
を任意の公倍数とする.
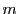 を
を 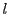 で割った商を
で割った商を 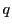 ,余りを
,余りを 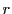 とすると
とすると
となる.
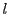 も
も 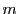 も
も  の倍数であるから
の倍数であるから 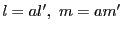 とおくと
とおくと
より, 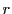 は
は  の倍数である.同様に
の倍数である.同様に
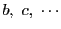 の倍数でもあり,
の倍数でもあり,
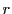 は
は
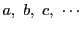 の公倍数となる.ところが
の公倍数となる.ところが 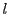 は正で最小の公倍数
であったから,もし
は正で最小の公倍数
であったから,もし 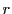 が0でないとすると,
が0でないとすると, 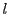 より小さい正の公倍数がある
ことになり,
より小さい正の公倍数がある
ことになり, 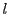 の最小性に反する.
の最小性に反する.
つまり 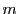 は
は 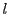 の倍数である.
の倍数である.
(2)
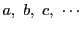 の最大公約数を
の最大公約数を 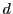 とし,
とし, 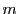 を任意の公約数とする.
を任意の公約数とする.
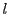 を
を 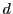 と
と 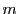 の最小公倍数とする.
の最小公倍数とする.  は
は 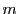 の倍数であり,
の倍数であり,
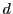 の倍数である.つまり
の倍数である.つまり 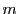 と
と 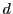 の公倍数であるから(1)より
の公倍数であるから(1)より  は
は 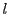 の
倍数である.同様に
の
倍数である.同様に
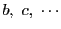 も
も 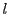 の倍数である.
つまり
の倍数である.
つまり 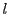 は
は
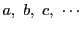 の公約数である.
の公約数である. 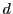 が最大の公約数なので,
が最大の公約数なので,
一方, 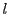 は
は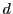 と
と 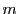 の最小公倍数なので
の最小公倍数なので 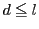
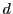 と
と 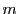 の最小公倍数
の最小公倍数 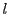 が
が 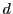 に一致した.
に一致した.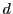 は
は 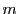 の倍数,
つまり任意の公約数
の倍数,
つまり任意の公約数 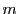 は最大公約数
は最大公約数 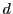 の約数である.
の約数である.
(3) 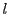 は
は 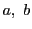 の最小公倍数であるから適当な整数
の最小公倍数であるから適当な整数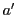 と
と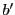 を用いて,
を用いて,
とおける.
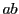 は
は 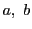 の公倍数だから(1)から
の公倍数だから(1)から 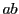 は
は 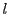 の倍数である.
の倍数である.
とする.よって
つまり 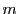 は
は 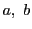 の公約数である.(2)より最大公約数
の公約数である.(2)より最大公約数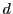 の約数なので,
の約数なので,
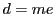 とおける.
とおける.
一方 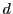 は
は 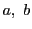 の最大公約数なので
の最大公約数なので
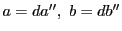 とおける.よって
とおける.よって
一方,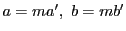 であるから
であるから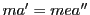 ,
,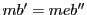 が成り立つ.
が成り立つ.
その結果,
ところがこれは 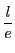 が
が 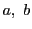 の公倍数であることを示している.
の公倍数であることを示している.
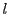 が最小の公倍数なのでその最小性により
が最小の公倍数なのでその最小性により 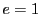 .
.
(4) 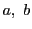 の最大公約数が 1 なので
の最大公約数が 1 なので 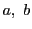 の最小公倍数は
の最小公倍数は 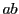 である.
仮定から
である.
仮定から 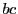 は
は  の倍数であり,したがって
の倍数であり,したがって  と
と 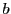 の公倍数である.
よって
の公倍数である.
よって 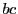 は
は 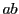 の倍数であり,
の倍数であり,
つまり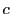 は
は  の倍数である.□
の倍数である.□
この定理の証明において,前節の「除法の定理」が基本定理として用いられてることが
わかる.日頃当然のように論証で使っていることが,「除法の定理」を基礎に厳密に示される.
整数
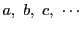 の最大公約数を,座標と混同する恐れのないときは
の最大公約数を,座標と混同する恐れのないときは
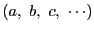 と書く.
と書く.
整数
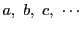 の最大公約数が1であることを簡単に「公約数をもたない」という.
この場合,
の最大公約数が1であることを簡単に「公約数をもたない」という.
この場合,
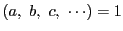 .
特に二つの整数
.
特に二つの整数 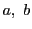 が公約数をもたないとき,つまり
が公約数をもたないとき,つまり 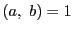 のとき,
のとき,
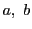 は互いに素であるという.
は互いに素であるという.


 次: ユークリッドの互除法
上: 約数と倍数
前: 約数と倍数
Aozora Gakuen
次: ユークリッドの互除法
上: 約数と倍数
前: 約数と倍数
Aozora Gakuen
![]() に共通な約数をそれらの整数の公約数という.
1は常に公約数である.
公約数の絶対値は
に共通な約数をそれらの整数の公約数という.
1は常に公約数である.
公約数の絶対値は
![]() のいずれの絶対値よりも大きくはないので,
公約数の中に最大のものがある.
それを最大公約数(greatest common measure 略して G.C.M.)という.■
のいずれの絶対値よりも大きくはないので,
公約数の中に最大のものがある.
それを最大公約数(greatest common measure 略して G.C.M.)という.■
![]() と
と![]() の最大公約数を座標などと混同する恐れのないときは
の最大公約数を座標などと混同する恐れのないときは
![]() と書く.
と書く.![]() のように用いる.
のように用いる.
![]() の最小公倍数を
の最小公倍数を ![]() とし,
とし, ![]() を任意の公倍数とする.
を任意の公倍数とする.
![]() を
を ![]() で割った商を
で割った商を ![]() ,余りを
,余りを ![]() とすると
とすると
![]() は
は ![]() の最大公約数なので
の最大公約数なので
![]() とおける.よって
とおける.よって
![]() であるから
であるから![]() ,
,![]() が成り立つ.
が成り立つ.
![]() の最大公約数を,座標と混同する恐れのないときは
の最大公約数を,座標と混同する恐れのないときは
![]() と書く.
と書く.
![]() の最大公約数が1であることを簡単に「公約数をもたない」という.
この場合,
の最大公約数が1であることを簡単に「公約数をもたない」という.
この場合,
![]() .
特に二つの整数
.
特に二つの整数 ![]() が公約数をもたないとき,つまり
が公約数をもたないとき,つまり ![]() のとき,
のとき,
![]() は互いに素であるという.
は互いに素であるという.