次: 指数 上: 原始根と指数 前: 原始根と指数

原始根

5で割った余りから0を除いた

$$1,\ 2,\ 3,\ 4$$

のうち，2と3は特別である．なぜか．

$$\begin{array}{l} 2^1=2\\ 2^2=4\equiv 4\quad (\bmod.\ ... ...\bmod.\ 5)\\ 3^4=81\equiv 1\quad (\bmod.\ 5) \end{array}$$

と順にべきを取っていくと$1,\ 2,\ 3,\ 4$をすべて作る． 1と4はそうではない．

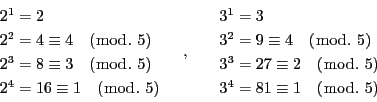
2と3を「5を法とする原始根」という．

剰余系の原始根

13を法とする剰余系から0を除いた各剰余を横に並べる． それぞれのべきを縦方向に順次書いてみる． 1が出ればそこからは同じことがくり返される．それは省略している．

$$\begin{array}{c\vert rrrrrrrrrrrr} 剰余a&1&2&3&4&5&6&7... ...&11&2&&&&6&\\ a^{12}&1&1&1&1&1&1&1&1&1&1&1&1 \end{array}$$

フェルマの定理によれば $p$ が素数で, $a$ が $p$ で割り切れないとき，

$$a^{p-1}\equiv 1\quad (\bmod.\ p)$$

である．したがって $a^{12}$ の段に1が並ぶのは当然であるが， 2，6，７，11 は12乗してはじめて1と合同であり， しかも途中の $１,\ a,\ a^2,\ \cdots,\ a^{11}$ が 13を法とする既約剰余系の代表の組となっている． そこで $a$ が $p-1$ 乗してはじめて1と合同になるとき， $a$ を $p$ を法としての原始根という． 略して $p$ の原始根ともいう．

さて「原始根」という呼び名はすでに「1の$n$乗根」で出ている． 複素数全体の中で $n$ 乗してはじめて1になるものを「1の原始( $n$ 乗)根」と 呼んだ． 今は $p$ を法とする剰余の集合

$$K=\{0,\ 1,\ 2,\ \cdots ,\ p-1\}$$

のなかで, $p-1$ 乗してはじめて1と合同になるものを考えている． この場合，$p$ を法とする剰余系の代表として数$a$ が $e$乗して1と合同になるなら，$e$ は $p-1$ の約数である． はじめて1と合同になるとき $e$ は $a$ の( $p$ を法とする)指数というのであった． 指数が $p-1$ となる場合にそれを原始根というのである．

上の集合 $K$ は $p$ 個の元からなる有限集合であるが， 和・差・積・商が定まる有限体である． また $K$ から0を除いた集合 $K^{\times}$ は乗法に関して群であり， 要素の個数は$p-1$個である．

次の定理が示すように，一般に素数$p$に対して原始根が存在し， その原始根の順次のべきから$K^{\times}$ のすべての元が得られる． つまり,原始根はこの「群を生成する」元である．

定理 28
     素数 $p$ を法として原始根が存在する． $r$ をその一つとすれば，

$$１,\ r,\ r^2,\ \cdots,\ r^{p-2}$$

は既約剰余系の一組である．■

証明     $a$ を $p$ を法とする既約剰余系の一つの代表である数とする．言いかえれば $a\not \equiv 0\quad (\bmod.\ p)$ をとる． $a$ の指数を $m$ とする． $a^m\equiv 1\quad (\bmod.\ p)$ なので

$$a^0=1,\ a^1,\ \cdots,\ a^{m-1}$$ (2.32)

はいずれも

$$x^m\equiv 1\quad (\bmod.\ p)$$ (2.33)

の解である．これらは互いに同じ剰余系に属さない． なぜなら, $1\le i \le m-1$ に対して

$$a^i\equiv a^j\quad (\bmod.\ p)\quad \iff\quad a^{i-j}\equiv 1\quad (\bmod.\ p)$$

である．定理 24 から $i-j$ は $m$ の倍数である． $-m+2\le i-j \le m-2$なので これは $i=j$ のときのみである． 定理14から(2.32)が(2.33)の解のすべてである．

さて $m=p-1$ なら $a$ 自身が原始根である． $m<p-1$ のとき． $a$ をもとに $m$ より大きい指数の数を構成できることを示す．

$p$ を法とする既約剰余系は $p-1$ 個あるので， この場合(2.32)のいずれとも異なる剰余系がある． そのような剰余系に属する数 $b$ をとる． $b$ の指数を $n$ とする． このとき $n$ は $m$ の約数でない．もし約数なら $b^m\equiv 1\quad (\bmod.\ p)$ となる． したがって $b$ も合同方程式(2.33)の解となり $b$ に関する仮定に反する． そこで
(1)    $(m,\ n)=1$ のとき． $ab$ の指数は $mn$ である．

なぜなら，まず $(ab)^{mn}=a^{mn}b^{mn}\equiv 1\quad (\bmod.\ p)$ であるが， 逆に $(ab)^x\equiv 1\quad (\bmod.\ p)$ とする． このとき

$$(ab)^{mx}\equiv b^{mx}\equiv 1\quad (\bmod.\ p)$$

定理 24 から $mx$ は $n$ の倍数であるが$(m,\ n)=1$ から $x$ が $n$ の倍数である．

同様に $x$ は $m$ の倍数でもあり， 定理 2 から$x$ は $m$ と $n$ の最小公倍数の倍数である．$(m,\ n)=1$ から最小公倍数は $mn$ ． ゆえに $ab$ の指数は $mn$ である． $mn>m$ より $p$ を法として $m$ より大きい指数の数が構成できた．
(2)    $(m,\ n)=d>1$ のとき． $m$ と $n$ の最小公倍数を $l$ とする． 練習問題6の(6)のように $l=m_0n_0,\ (m_0,\ n_0)=1$ で$m_0$は $m$ の約数， $n_0$は $n$ の約数となるものをとる． このとき $a^{ \frac{m}{m_0}},\ b^{ \frac{n}{n_0}}$ はそれぞれ指数が $m_0,\ n_0$である．$(m_0,\ n_0)=1$より $a^{\frac{m}{m_0}}b^{\frac{n}{n_0}}$ の指数は$m_0n_0=l$． $n$ は $m$ の約数ではないので$l>m$ ．やはり $p$ を法として $m$ より大きい指数の数が構成できた．

真に増加する指数の列ができ，しかも $p-1$ を越えないので有限回の操作で必ず指数 $p-1$ の数が構成できる．つまり原始根 $r$ は必ず存在する． すでに見たように(2.32)は互いに合同でない．したがって

$$１,\ r,\ r^2,\ \cdots,\ r^{p-2}$$

も互いに合同でない．つまりこれらは $p-1$ 個の既約剰余系の一組の代表である．□

既約剰余系でみれば$(k,\ p-1)=1$であることが $r^k$ が原始根 であるための必要十分条件である．したがって原始根は$\varphi(p-1)$個ある．

例 2.5.1        $\varphi(13-1)=4$なので四つある．実際 $2,\ 6,\ 7,\ 11$

次: 指数 上: 原始根と指数 前: 原始根と指数