次: 多項式環 上: 除法のできる環 前: 除法のできる環

ユークリッド整域

整数環$\mathbb{Z}$は次のような性質がある．

(1)    $\mathbb{Z}$の二つの要素$a,\ b$について$ab=0$ならば $a=0$または$b=0$が成り立つ． いずれもが 0 ではない二つの要素$a,\ b$ で，$ab=0$となるものがあれば，$a$を左零因子，$b$を右零因子という．左零因子，右零因子をまとめて零因子という．

これは行列からなる環では成り立たない．二次行列の集合$A$は行列の和と積で環である． 行列環$A$では

$$\matrix{0}{1}{0}{1}\matrix{1}{0}{0}{0}=\matrix{0}{0}{0}{0}$$

のように零因子がある．

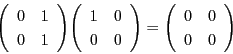
零因子が存在しないような環を整域という．整数環$\mathbb{Z}$は整域である．

(2)    $\mathbb{Z}$には元$a$について大きさ$\vert a\vert$ が定義されていて，任意の$a(\not=0),\ b$について

$$b=qa+r\quad 0\le r<\vert a\vert$$

となる元$q,\ r$が一意に存在する．

環$R$には，その要素$a$に対して大きさといわれる0以上の実数が定まり， (1)と(2)の両方が成り立つなら， その環$R$をユークリッド整域，あるいはユークリッド環という． 大きさを絶対値とすることで，整数環はユークリッド整域である． 整数環は除法のできる整域である．

本節では，整数環以外に除法のできる整域を二つ考えよう．

一つは多項式からなる環である．ここで多項式は$3x$のような単項式も含め整式と同じ意味に用いる．多項式の集合では、整数と同じく因数分解ができ，かつ素因数分解の(定数倍を除く)一意性が成り立つ． なぜ多項式でも素因数分解の一意性がなり立つのか．それは多項式では除法の定理が成り立つからである．結局は整数の場合と同じく，除法の定理が成立することが根拠なのである．

もう一つは、実部、虚部がそれぞれ整数であるような複素数からなる集合

$$\{a+bi\ \vert\ a,\ b \in \mathbb{Z}\}$$

である．これをガウス整数環という． 『数論初歩』では略してガウス環ともいうこともある． 代数学の一分野の環論では，素数(厳密には素元という)への分解が(単数を除いて)一意である整域のことをガウス環という．