

 次: 差で閉じた部分集合
上: 一次不定方程式
前: 一次不定方程式
次: 差で閉じた部分集合
上: 一次不定方程式
前: 一次不定方程式
未知数が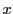 と
と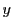 ,あるいは
,あるいは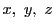 など2個以上あり,係数が整数である方程式,
例えば
など2個以上あり,係数が整数である方程式,
例えば
のようなものでは,実数の解は無数にある.解が定まらないので不定方程式という.
ところが,これらの方程式を満たす整数の組となると,
有限個であったり,すべてが書き下せたり,あるいは存在しなかったり,さまざまに変化する.不定方程式の整数解すべてを求めることはできるのか.
一般的に書くことができるのか.これが整数の主要な問題の一つである.
とくに一次不定方程式:
の整数解が重要なテーマである.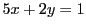 の整数解という問題では
の整数解という問題では
といくつもある.すべての解を求める,あるいは解の一般形を求めるという問題が生まれる.
さらに,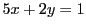 は暗算で解が一組は求まったが,
は暗算で解が一組は求まったが,
となると,すぐには見いだせないし,そもそも解の存在からして明らかではない.
どのような条件で解が存在するのか.
一次不定方程式の解の存在条件と,すべての解を求める問題を解決しよう.
ここでそのうち重要な二つを紹介する.
Aozora
2015-03-02