

 次: 整式の約数・倍数
上: 整式の整数論
前: 整式の整数論
次: 整式の約数・倍数
上: 整式の整数論
前: 整式の整数論
以上の議論は整式の場合にもそのままあてはまる.
実数係数の整式の集合を変数を明示して![$\mathbb{R}[x]$](images/img493.gif) と表そう.
また係数を有理数にかぎるときは
と表そう.
また係数を有理数にかぎるときは![$\mathbb{Q}[x]$](images/img494.gif) と表す.
以下のことは
と表す.
以下のことは
![$\mathbb{R}[x]$](images/img493.gif) で考えても,
で考えても,![$\mathbb{Q}[x]$](images/img494.gif) で考えても,
また複素数で考え
で考えても,
また複素数で考え![$\mathbb{C}[x]$](images/img495.gif) としても同じことである.
そこで
としても同じことである.
そこで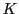 を有理数の集合
を有理数の集合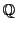 ,
実数の集合
,
実数の集合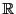 ,複素数の集合
,複素数の集合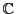 のいずれかを表すものとし,
これからは
のいずれかを表すものとし,
これからは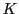 に係数をもつ整式の集合
に係数をもつ整式の集合![$K[x]$](images/img499.gif) を考えることにしよう.
を考えることにしよう.
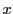 の整式は,つぎの除法の基本性質をもつ.
ここで
の整式は,つぎの除法の基本性質をもつ.
ここで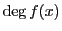 は整式
は整式 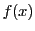 の次数を表す.
の次数を表す.
定理 15
整式
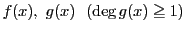
がある.
となる整式
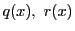
がただ1組存在する.
証明
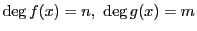 とする.
条件を満たす
とする.
条件を満たす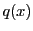 と
と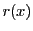 の存在を
の存在を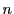 についての数学的帰納法で示す.
についての数学的帰納法で示す.
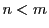 なら
なら
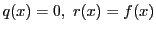 で成立.
で成立.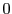 から
から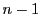 で成立とする.
で成立とする.
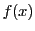 と
と 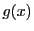 の
の 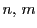 次の項をそれぞれ
次の項をそれぞれ 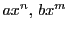 とする.
とする.
と定めれば,
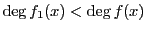 である.
帰納法の仮定から,
である.
帰納法の仮定から,
となる
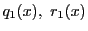 が存在する.
が存在する.
となるので,
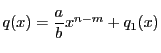 ,
,
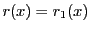 とおけば定理の等式を満たす.
とおけば定理の等式を満たす.
これが1組しかないことを示す.2組あったとする.
すると,
となる.
もし
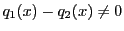 なら
なら
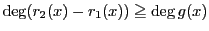 である.
である.
ところが一方,
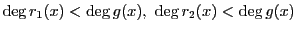 だから,
だから,
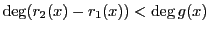 .これは矛盾.
.これは矛盾.
ゆえに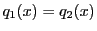 .この結果
.この結果
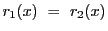 となる.
(証明終わり)
となる.
(証明終わり)
Aozora
2015-03-02
![]() の整式は,つぎの除法の基本性質をもつ.
ここで
の整式は,つぎの除法の基本性質をもつ.
ここで![]() は整式
は整式 ![]() の次数を表す.
の次数を表す.
![]() なら
なら
![]() で成立.
で成立.![]() から
から![]() で成立とする.
で成立とする.
![]() と
と ![]() の
の ![]() 次の項をそれぞれ
次の項をそれぞれ ![]() とする.
とする.
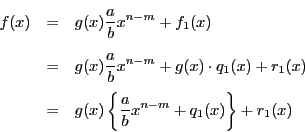
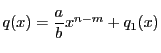 ,
,
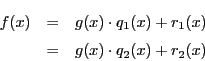
![]() だから,
だから,
![]() .これは矛盾.
.これは矛盾.
![]() .この結果
.この結果
![]() となる.
(証明終わり)
となる.
(証明終わり)