

 次: 約数・倍数と最大公約数
上: 整数の約数と倍数
前: 整数の約数と倍数
次: 約数・倍数と最大公約数
上: 整数の約数と倍数
前: 整数の約数と倍数
自然数を基礎にして,さらに0と負の数を加えて整数の集合ができる.
整数の集合を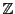 とする.
とする.
である.
詳しくいうと,自然数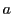 に対して
に対して
となる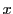 を0と表す.さらにこの0を用いて
を0と表す.さらにこの0を用いて
となる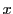 を
を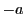 と表す.
と表す.
自然数に,このようにして得られる数をすべて加えて得られる集合が整数の集合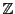 である.
0に自然数を加えて得られる整数を正の整数,
0から自然数を引いて得られる整数を負の整数,という.
正の整数と自然数は同じ意味になる.
整数の集合
である.
0に自然数を加えて得られる整数を正の整数,
0から自然数を引いて得られる整数を負の整数,という.
正の整数と自然数は同じ意味になる.
整数の集合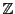 は,加法,減法,乗法に関して閉じている.
は,加法,減法,乗法に関して閉じている.
整数の集合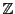 は,演算の除法(割り算)に関しては閉じていない.
整数では除法をおこなうとその結果が
は,演算の除法(割り算)に関しては閉じていない.
整数では除法をおこなうとその結果が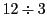 のように
のように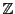 に属する場合と,
に属する場合と,
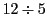 のように属さない場合がある.
属さない場合は
のように属さない場合がある.
属さない場合は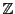 の中では余りが出る.
の中では余りが出る.
割り算を行うとき,まずどのように考えるか思い起こそう.
例えば75を6で割るとき,6が何回分75の中にあるかを考えるのではないか.
そして,6にその数を乗じた数を75から引く.それが余りになる.
次の定理と証明はそれを定式化したものである.
定理 1
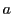
を整数,
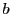
を0でない正の整数とする.このとき,
となる整数
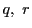
がただ1組存在する.
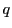
を
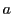
を
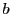
で割った
商,
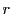
を
余りという.
証明
正の整数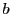 に対して,整数
に対して,整数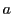 は次のような不等式のいずれか一つに入る.
は次のような不等式のいずれか一つに入る.
いいかえると整数 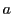 と正整数
と正整数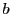 に対して,
に対して,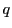 は整数を動くとすると,
は整数を動くとすると,
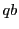 は
は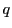 に関して単調増加なので
に関して単調増加なので
となる整数 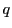 がただ一つ存在する.
がただ一つ存在する.
この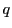 に対して
に対して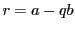 とおく.
とおく.
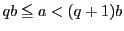 より
より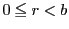 であり
であり
が成り立つ.存在は示せた.一つしかないことを示す.
このような 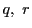 が二通りあったとし,
が二通りあったとし,
とする.これから
よって,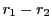 は
は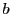 の倍数である.
ところが
の倍数である.
ところが
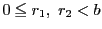 なので,
なので,
この範囲の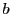 の倍数は0しかない.よって
の倍数は0しかない.よって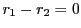 .
これから
.
これから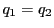 となり,一通りしかないことが示された.
(証明終わり)
となり,一通りしかないことが示された.
(証明終わり)
このように整数の割り算では,整数のなかでの商と余りが一通りに定まる.
整数の論証の基本はこの除法に関する性質が根拠になる.
除法は整数の論証の基礎である.論証のなかで除法を適切に使えることが大切だ.
Aozora
2015-03-02
![]() である.
0に自然数を加えて得られる整数を正の整数,
0から自然数を引いて得られる整数を負の整数,という.
正の整数と自然数は同じ意味になる.
整数の集合
である.
0に自然数を加えて得られる整数を正の整数,
0から自然数を引いて得られる整数を負の整数,という.
正の整数と自然数は同じ意味になる.
整数の集合![]() は,加法,減法,乗法に関して閉じている.
は,加法,減法,乗法に関して閉じている.
![]() に対して
に対して![]() とおく.
とおく.
![]() より
より![]() であり
であり