南海 実数を構成するためには,「連続性」を考えなければならない.
日本の高校の教科書では証明なしに次のことが成り立つとされる.
なぜそんなことが保証されるのか,と考えたことはないだろうか.
史織 当然成り立つものとして考えていますが, 確かにこれはその後に習う「中間値の定理」や,「ロルの定理」,「平均値の定理」の基礎になっています.
南海 ときどき,基礎分野になっているのに証明なしに使っていることを,考えてみるのはよいことだ. もちろん,数学の歴史でもはじめから実数について今日のような理解があったわけではない. デデキント(Julius Wilhelm Richard Dedekind, 1831〜1916)や カントール(Georg Cantor,1845〜1918)らによって実数論や集合論が開拓された.岩波文庫には デデキントの『連続性と無理数』の翻訳がある.高校生が読んですべてがわかるわけではないが,しかし読める. デデキントがどのようなところから実数論を考えていったかよくわかる.
数学は,ある面ではそういう厳密性とは独立に進み,あるときにはその理論を支えるために厳密性を求めて進み, こうして相互に発展してきた.
連続関数の閉区間における最大値,最小値の存在を保証する根拠となっているのは, 実数の連続性といわれる性質だ. 実数の構成についていくつか考えてみよう.
日本の高校でも「集合」の概念は習う. しかし,実際に扱うのは要素の個数が有限である場合がほとんどだった.
実は,集合は無限集合を考えるとき,面白く不思議なことが起こる.
自然数の集合 ![]() ,正の偶数の集合
,正の偶数の集合![]() という2つの集合を考えよう.
という2つの集合を考えよう.
無限集合ではこのように部分集合の各要素と全体集合の各要素の間に ![]() の対応ができることがある.
の対応ができることがある.
史織
有理数と自然数の間にも ![]() 対応があるということを聞いたことがあります.
対応の仕方は覚えていません.
対応があるということを聞いたことがあります.
対応の仕方は覚えていません.
南海
![]() を有理数の集合としよう.次のようにすると,
を有理数の集合としよう.次のようにすると,
![]() の各要素と
の各要素と ![]() の各要素の間に
の各要素の間に ![]() の対応が付けられる.
第1象限と第2象限の格子点を
の対応が付けられる.
第1象限と第2象限の格子点を ![]() から始めて図の矢印のようにとっていく.
格子点
から始めて図の矢印のようにとっていく.
格子点 ![]() に対して有理数
に対して有理数 ![]() を対応させると有理数の列ができる.
を対応させると有理数の列ができる.
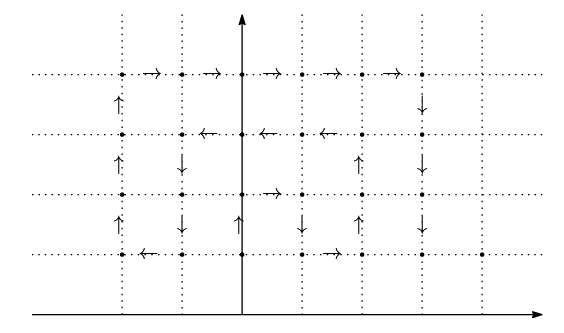
このように自然数と ![]() の対応が作れる無限集合を「可付番である」という.
の対応が作れる無限集合を「可付番である」という.
ところが,である.カントールは「実数の集合は可付番でない」ことを示したのだ. カントールは三角関数の級数の研究から集合論を創始. また,位相空間論の基礎を築いた.現代的な数学のはじまりとなったものだ.
それがまた背理法で示されるのだ.
区間 [0,1]つまり 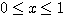 を満たす実数の集合が可付番であると仮定する.
つまり
を満たす実数の集合が可付番であると仮定する.
つまり 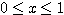 を満たす実数全体に番号を付けて次のようにできるとする.
を満たす実数全体に番号を付けて次のようにできるとする.
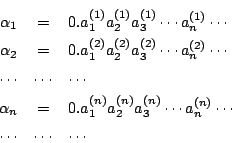
のようにできる.ここに ![]() は
は ![]() 番目の小数の,小数第
番目の小数の,小数第 ![]() 位の数を表している.
位の数を表している.
この対角線に並んでいる数 ![]() に対して数
に対して数 ![]() を次のように作る.
を次のように作る.
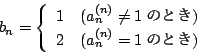
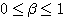 である.しかし
である.しかし 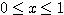 を満たす実数の全体という仮定と矛盾した.つまり
を満たす実数の全体という仮定と矛盾した.つまり 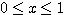 を満たす実数の集合は
可付番でないことが示された.この背理法を「カントールの対角線論法」という.
実数は有理数よりこの意味でたくさんあるのだ!
を満たす実数の集合は
可付番でないことが示された.この背理法を「カントールの対角線論法」という.
実数は有理数よりこの意味でたくさんあるのだ!