南海 今年になって特に思うのだが，確率の授業のときの生徒諸君の表情が生きていない． 他の分野では，「うん，うん」とうなずいたり，方針がわかれば自分で計算をはじめたりと， いろいろ反応があるのだが，確率のときはおしなべて皆，無表情だ．
史織 確率は，あっているのか間違っているのかよくわからないままに解いています． また，すべての確率の和が1ということ以外には，解答を検算する方法もなくて，答えに確信が持てません．
南海 確率は，高校数学の中では現実との接点をもつ数少ない分野だ， 問題文を読んでそれが事実どのような現実(試行)を問題にしているのかを読み取る力が必要だ． つまり確率問題は文章の読解力を含む総合的な力が必要なのだ． 高校生諸君の，そんな現実把握力が急速に落ち込んでいるようにも思われる． 同時に，教える側の力がどんどん低下している．悪循環だ．
学校では確率の問題が，順列組合せの場合の数の応用問題のように扱われ，計算練習が中心である． が，それではいつまでたっても「確率が苦手」を克服することができない．
せめて青空学園に縁があった人は，確率とは何かを理解し，確率問題が解ける総合的な力をつけてもらいたい．
史織 現実との接点とは，どういうことですか．
南海 確率論的にいえば，「何が同様に確からしいのか」を考えなければならないということだ．
次の例題はよく出てくる．解答は正しいだろうか．
解答：区別がつかないので出方は(表，表)，(表，裏)，(裏，裏)の3通り．
2つの表裏が一致する場合は2通り．よって求める確率は 
．□
史織 (表，表)，(表，裏)，(裏，裏)の3通り出方は同様に確からしいわけではありません． ところが，確率の計算では， 該当する出方の総数を，すべての出方の場合の数で割っています． これができるのは，すべての出方が同様に確からしいときだけです．
つまり，「区別がないのだから(表，表)，(表，裏)，(裏，裏)の3通りは同様に確からしい」と 勝手にしていることです．実際問題としてこれは同様に確からしくありません．
南海 数多くの試行を繰りかえせば(表，表)に対して(表，裏)の組はおよそ2倍出やすいことがわかる． だが，これで終わりにせずにここでいろんなことを考えなければならない．
数学としては何を根拠にそのように断定できるのか．
史織
1枚の硬貨を投げたときに，表がでるか裏がでるかが同様に確からしい，つまり表が出る確率，裏が出る確率が
それぞれ
．これが根拠だと思います．
すると2枚の硬貨を投げるのだから，それぞれの硬貨の表裏の組合せ，
「(表，表)，(表，裏)，(裏，表)，(裏，裏)」の4つが同様に確からしい．そしてこの4つの事象が根元事象である．
事象の総数が4であるから，各確率はそれぞれ
である．
サイコロを区別するかしないかは人間の側の問題で，1枚の硬貨の裏と表が同様に確からしいとするかぎり， それぞれの硬貨の裏表を考えざるを得ないし，2枚の硬貨は区別しなければならないと思います．
南海 その通りだ．さらに2枚の硬貨それぞれの裏表が互いの他方の裏表に関係しないことが大切だ．
硬貨に細工をして「(表，表)，(表，裏)，(裏，裏)」が同様に確からしくすることもできるかもしれない．
例えば2枚を次々に投げることにして，1枚目の硬貨は表と裏が出る確率が等しいが，2枚目の硬貨は，
1枚目と同じ面が出る確率がで，
1枚目と異なる面が出る確率が
であるとする．
その場合は，「(表，表)，(表，裏)，(裏，表)，(裏，裏)」の確率が
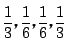であるようになり，
「(表，表)，(表，裏)，(裏，裏)」がいずれも確率になる．
しかし，この場合，2つの硬貨の一方が表か裏が出るかにしたがって， 他方の硬貨の表裏が出る確率が変化しなければならない． つまり，2枚目の硬貨の表裏の出る確率が1枚目の確率から独立していない． 逆に2枚の硬貨の表裏の確率は互いに独立で，相手の表裏には影響されないとするならば，これは不可能である．
通常，このように硬貨2枚の試行では
史織 ずいぶん難しいですね．
南海 というより，これが現実だ，ということ．