方程式は(5)で考える.
![]() は
は![]() に分解されるわけだが,
これらの作用に関する係数
に分解されるわけだが,
これらの作用に関する係数
耕介
そうか.
![]() の任意の要素で考えるよりも,
の任意の要素で考えるよりも,
![]() の要素でどのようになるかを確認した方が簡明です.
の要素でどのようになるかを確認した方が簡明です.
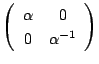 の場合.
の場合.![]() を
を
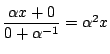 に置きかえ,
に置きかえ,
![]() をかければよい.
をかければよい.
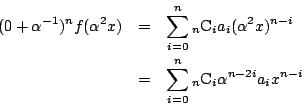
したがって対応する![]() 次の行列は
次の行列は
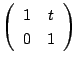 の場合.
の場合.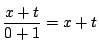 に置きかえればいい.
に置きかえればいい.
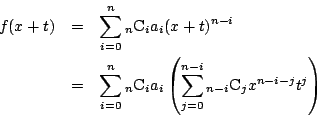
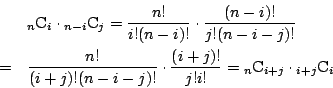
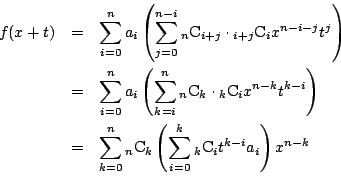

南海
これに対応する微分作用素も決めておこう.
![]() のときの微分作用素の決め方と同様に考えればよい.
のときの微分作用素の決め方と同様に考えればよい.
上の
![]() の変換で
もとの
の変換で
もとの![]() に代入するのは
に代入するのは
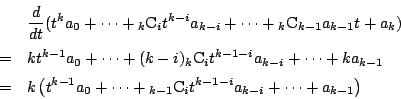
耕介
ということは,![]() で微分して0となることが,
で微分して0となることが,
![]() と同値であるような,微分作用素
と同値であるような,微分作用素![]() は
は
南海
そう.そしてこれを対称に入れ替えて![]() が作られる.
が作られる.
次に単項式
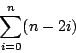
耕介
![]() であることが
であることが![]() 不変であることを意味するのは,
2次の場合と同じです.
微分作用素
不変であることを意味するのは,
2次の場合と同じです.
微分作用素![]() のどの項も,
単項式の操作としては
のどの項も,
単項式の操作としては![]() を
を![]() に置きかえるので,
に置きかえるので,
![]() は2増えます.
そこで,
は2増えます.
そこで,
![]() 個の変数の整式の集合
個の変数の整式の集合
南海 ここで証明は出来ないが,次の2つが成り立つ.
耕介
すると,![]() の作用に関する方程式の不変式は,
やはり
の作用に関する方程式の不変式は,
やはり![]() の核になります.
2次の場合と同様にしていけば,
それぞれの次数に関する方程式の不変式が得られるのですか.
の核になります.
2次の場合と同様にしていけば,
それぞれの次数に関する方程式の不変式が得られるのですか.
南海 2の場合は比較的簡単であったが,次数が増えると急速に複雑になる. 3次4次の場合の結果のみ記しておこう.
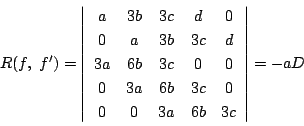
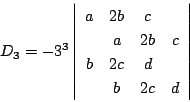

4次の場合は判別式よりも低い次数で不変式が見つかる.
2次の単項式で![]() となるもの,
つまり
となるもの,
つまり![]() の基底は
の基底は
3次の単項式で![]() となるもの,
つまり
となるもの,
つまり![]() の基底は
の基底は
この2つが2次と3次の不変式で,これらで生成されたものが,
4次方程式の不変式である.ちなみに判別式![]() は
は
耕介 このようにして順にやっていくのは大変ではありませんか.
南海 そうだ. 次数が大きくなると,不変式は多くなり複雑になっていく.
2変数![]() 次の整式
次の整式![]() に対し,
に対し,
耕介
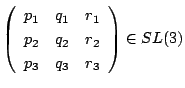 の作用での不変式ですね.
の作用での不変式ですね.
南海 そうだ.後に抽象代数学の旗手となった女性数学者の エミー・ネーター(Amalie Emmy Noether 1882〜1935)は, この2変数で4次の場合に不変式を調べ, 331個の不変式を書きだし,それらによってすべての不変式が書き表せる ことを証明し,ゴルダンのもとで1907年に学位論文としている.
耕介 すごいですね. でもきりがありませんね.
南海 不変式論は,このように具体的に構成する段階の中から, 新しい考え方をきりひらいていった. そのことが大切なので,次に新しい発展について, 話そう.