次： チェビシフの多項式 上： 原始多項式 前： 因数分解のアルゴリズム

代数的整数

耕一　 ところで，最初の例題にかえって質問です． 整数係数で最高次の項の係数が1である多項式を$f(x)$とする． 有理数$\alpha$が$f(x)=0$の解なら$\alpha$は整数である，という事実の意味がよくわかりません．

南海　 以下整数係数の多項式を考える．そこでいわゆる「整数」だが，これは 最高次数の係数が1の一次式の解になっていないか．

耕一　 3は$x-3=0$の解，$-5$は$x+5=0$の解，ということですね．最高次数の係数が1でない 既約多項式の解は整数でない有理数になる．

南海　 そこで，次数が1より大きくても最高次の項の係数が1である整数係数の多項式$f(x)$に対し，方程式$f(x)=0$の解となる複素数を「(代数的)整数」と呼ぶのだ．

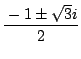耕一　 えっ．すると$\sqrt{2}$は$x^2-2=0$の解だから代数的整数， 虚数$i$も$x^2+1=0$解だから代数的整数，$x^2+x+1=0$の解 $\dfrac{-1\pm \sqrt{3}i}{2}$も 代数的整数ということになります．

南海　 その通りなのだ．いままでの整数は区別していうときは「有理整数」呼ぶ． 代数的整数の理論が19世紀末から20世紀にかけて大発展した．われわれの『数論初歩』に 引き続く分野なのだ．高木貞治はこの分野で「類体論」と呼ばれる決定的な仕事をした．

耕一　 でも整数という以上は，和差積で得られるものはすべて整数にならなければならない． $a$と$b$を整数とすると，集合

$$\{ a+b\sqrt{2} \}$$

は全部代数的整数?　ですね． $a+b\sqrt{2}$と$a-b\sqrt{2}$は和が$2a$，積が$a^2-2b^2$だから 最高次数の係数が1の多項式からできる方程式

$$x^2-2ax+a^2-2b^2=0$$

の解になっています．

こういう世界を考えていくのですね．

南海　 そう．代数的整数の世界では有理整数の世界とは違ったことがいろいろ起こる． 例えば，因数分解の一意性が成り立たない．

耕一　 代数的整数$\alpha$が

$$\alpha=st=uv$$

と異なる因数分解をもつということですか．

南海　 正確には，代数的整数の世界の「素数」を定義しなければならない． そしてある種の代数的整数では，一方に現れて一方に現れない素数がある2種の因数分解が 可能なのだ．しかしこの話はここまでにしておこう．

さて，質問のあった

整数係数で最高次の項の係数が1である多項式を$f(x)$とする． 有理数$\alpha$が$f(x)=0$の解なら$\alpha$は整数である，という事実の意味

であるが，これは

$$代数的整数であって有理数でもあるものは有理整数である．$$

ことを意味している．

耕一　 代数的整数と有理数の共通部分がちょうど有理整数ということですね．