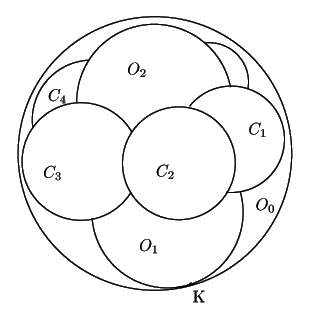
 互いに接する3個の球
互いに接する3個の球
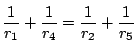 が成立する.
が成立する.
イギリスのノーベル化学賞受賞者Sir Frederik Soddy(1877-1956)は雑誌 Nature(1936)において球の接触問題に関してThe Hexlet(6球連鎖)なる次の定理を発表した.
これには4個の互いに接する球に関する定理が使われている. 発表当時は見事な定理として世界的に話題になった. ところが,この定理は,百年以上前の1822年, 相州(現在の神奈川県)の寒川神社に掲げられた算額にすでに記されていた. これは『日本の幾何』に詳しい. またウエブサイト Japanese Temple Geometry にも英文で紹介されている.
 互いに接する3個の球
互いに接する3個の球
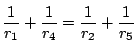 が成立する.
が成立する.
南海
方針としては,![]() の接点を
の接点を![]() とし,
とし,![]() での反転を考える.
での反転を考える.
太郎
円![]() と円
と円![]() はいずれも
はいずれも![]() と中心を結ぶ直線と直交している.
従ってその反転平面
と中心を結ぶ直線と直交している.
従ってその反転平面![]() もこの直線に直交し,従って平行である.
もこの直線に直交し,従って平行である.
![]() はいずれもこの平行面に挟まれ,
かつ面に接しているので半径はすべて等しい.
はいずれもこの平行面に挟まれ,
かつ面に接しているので半径はすべて等しい.
![]() の周りに互いに半径が等しい球が互いに外接するので,
それらの中心を通る平面での断面の円を考えることにより,
周りの球の個数は6個以外にありえない.
の周りに互いに半径が等しい球が互いに外接するので,
それらの中心を通る平面での断面の円を考えることにより,
周りの球の個数は6個以外にありえない.
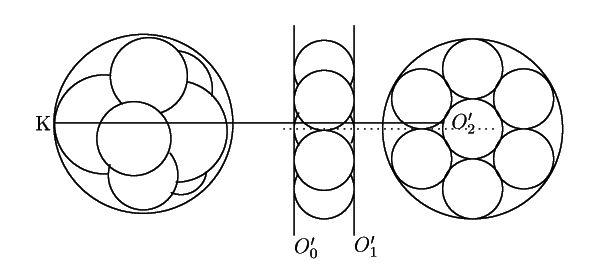
つぎに二円  について,これらの中心と反転の中心
について,これらの中心と反転の中心![]() でできる平面での切断面を考えると,そこでは円の反転になっている.
6個の円に外接する円をあわせて考えることで,
定理7の証明と同様に
でできる平面での切断面を考えると,そこでは円の反転になっている.
6個の円に外接する円をあわせて考えることで,
定理7の証明と同様に
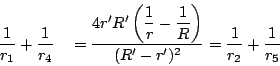
南海 球の半径の逆数とは曲率に他ならないことにも注意しよう. 和算家の証明は,反転法ではなくいわゆるデカルトの円定理, およびその一般化である三次元球の定理を用いている. 円定理もまた非常に面白いので,これは次の機会に考えよう.