複素数平面上の3点を
とおき,
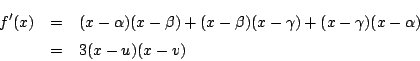
とおく.
このとき次のことが成り立つ.
-
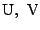 を焦点とし,
を焦点とし,
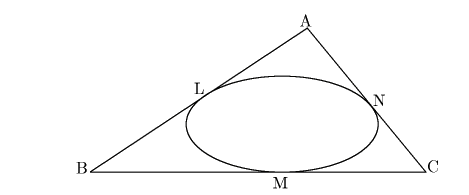
 に各辺の中点で
内接する楕円が存在する.
に各辺の中点で
内接する楕円が存在する.
- この楕円は
 に内接する楕円のなかで面積最大のも
のである.
に内接する楕円のなかで面積最大のも
のである.
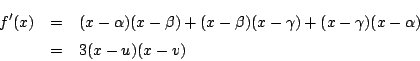
このとき次のことが成り立つ.
南海 まず次の補題を確認しておこう.
補題

定理3の証明
1.について
![]() ,
, ![]() ,
, ![]() の中点をそれぞれ
の中点をそれぞれ
![]() ,
, ![]() ,
, ![]() とする.
とする.
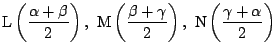 である.
1.を示すためには次の2点を示せばよい.
である.
1.を示すためには次の2点を示せばよい.
解と係数の関係から
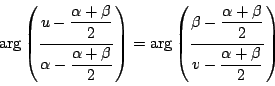
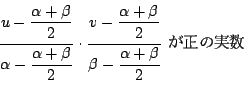
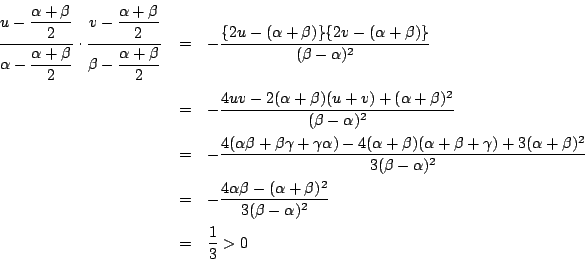
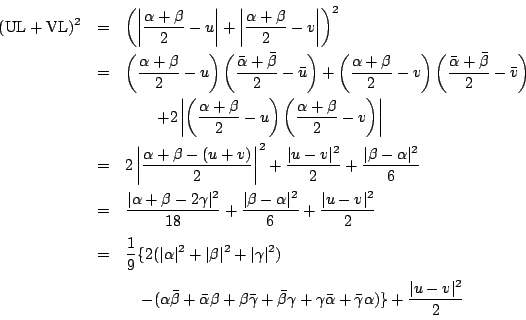
したがって確かに題意を満たす楕円が存在する.□