- 二円の交点を通り,かつ点
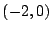 を通る円を求めよ.
を通る円を求めよ.
- 二円の交点を通る直線を求めよ.
拓生 最近,二つの円の2交点とさらにある定点を 通るような円を求める問題を学校で習いました.
例えば次の問題です.
この問題は,次のよう解きました.
解答
1 が点 ![]() を通るので,
を通るので, 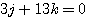 .
.
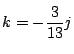 を代入して,
を代入して, ![]() で割り分母を払って整理すると,
で割り分母を払って整理すると,
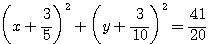
よって,
南海
教科書では普通,
![]() と
置きます.どうして
と
置きます.どうして
![]() としたのですか.
としたのですか.
拓生
教科書の置き方では二の円自身が求めるもので
ある場合 ![]() が解なしになってしまうので,このようにしました.実際は
が解なしになってしまうので,このようにしました.実際は 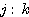 の比で決まるの
で,場合分けすれば二つの文字は必要ないのですが.
の比で決まるの
で,場合分けすれば二つの文字は必要ないのですが.
南海
いや,ここにある問題は,直線を ![]() と
表すと
と
表すと ![]() 型の直線が表せないが
型の直線が表せないが ![]() と置くとすべて表せ,
と置くとすべて表せ, ![]() の比で直線
が決まる,という問題と本質は同じです.
の比で直線
が決まる,という問題と本質は同じです.
拓生 なるほど,少しわかります.
南海 これについては別にまた考えましょう.
ところで君の質問は?