2定点
![]() ,
,
![]() と,
と, ![]() 軸上を動く点
軸上を動く点 ![]() とがある.
とがある.
![]() とする.
とする.
-
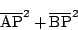
が最小になるような点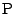 の座標を求めよ.
の座標を求めよ.
-
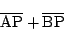
が最小になるような点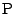 の座標を求めよ.
の座標を求めよ.
2定点
![]() ,
,
![]() と,
と, ![]() 軸上を動く点
軸上を動く点 ![]() とがある.
とがある.
![]() とする.
とする.
これは解けました.解答です.
解答
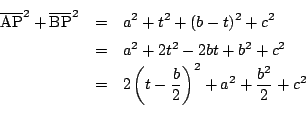
![]() と
と ![]() を結ぶ直線は,
を結ぶ直線は,
![]() とおいて,
とおいて,
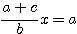 .よって
.よって
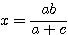
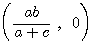 .□
.□
さらにもう一問です.
頂点の座標が
![]() ,
,
![]() ,
,
![]() である三角形
である三角形
![]() がある.座標平面上の任意の点
がある.座標平面上の任意の点 ![]() に対して,
に対して,
問題そのものはできました.解答です.
解答
![]() とおく.
とおく.
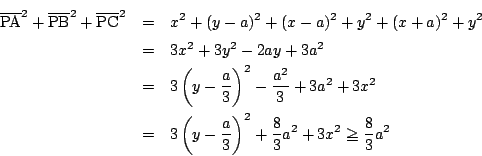
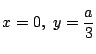 , つまり
, つまり
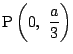 のとき.□
のとき.□
2番の問題の最小値を与える点は, 三角形 ![]() の重心で, 問題のような特別な点でなくても,
一般的に「3点への距離の二乗の和が最小になる点は重心です」.
の重心で, 問題のような特別な点でなくても,
一般的に「3点への距離の二乗の和が最小になる点は重心です」.
南海 その通り. 一般に3点からの距離の和を最小にする点は, 3点を頂点とする三角形の重心です.
拓生 はい.これは結局, 二次関数の最小問題です.
南海 で, 何がわからんのか.
拓生
問題の1番と2番を見比べると, 三点からの 距離の和 を最小にする
点 ![]() はどのような点なのか, 作図はできるのか, という問題が浮かびあがります.これは
解けるのでしょうか.
はどのような点なのか, 作図はできるのか, という問題が浮かびあがります.これは
解けるのでしょうか.
南海 そういうことか.与えられた問題が解けたことに満足せず, 問題の型を見比 べて新しい問題を見いだす, というのはすばらしいことだ.
だいたい教科書や問題集は解ける問題ばかり載せているが, そのすぐそばにこのようにして 問題を発見すれば, 難しい問題が潜んでいることが多いのだ.
三点からの距離の和が最小となる点を作図せよというわけだ.これは結構てごわい問題なんだ.
拓生 よく知られた問題ですか.
南海 この距離の和を最小にする点を「フェルマ点」と言ってな. つまりはあのフェルマ先生が研究したのだよ.