次: 三角形の成立条件と距離の公理 上: 計量ということ 前: 計量ということ

三平方の定理

美樹　 数学Iで「図形と計量」という単元があります． 三角比の定義を習い，三角比を用いて長さや面積，体積を求めます． 要するに三角比なのですが， 三角比と計量の関係がよくわかりません．

南海　 これまでは「三角比」としてやってきたことが「図形と計量」と変わった． その意図は教科書からはあまり伝わってこない． 中学課程では以前から「図形と計量」という単元があったようだが， その一部を高校に移すにあたって， 単元の名称も「三角比」から「図形と計量」になったようだ．

それはともかく，せっかく「計量」ということを高校でやるのだから， 計量ということについてもう少し深めて考えなければ意味がない．

計量は三角比と一緒に考えるよりも， 三角関数として加法定理とあわせて考えることでその意味がよくわかる。

計量の入り口は三平方の定理． これはどのような定理か．また証明は出来るか．

美樹　 ピタゴラスの定理ともいわれている定理です．

定理 1

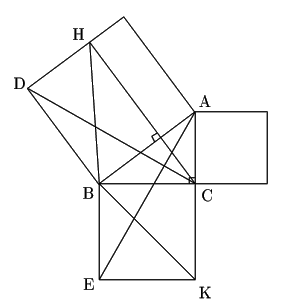
直角三角形の各辺に，その辺を一辺とする正方形を作ると， 斜辺上の正方形の面積は，他の2つの辺上の正方形の面積の和に等しい．

証明
図のように点に名前をつけます． $\bigtriangleup \mathrm{BEA}$と $\bigtriangleup \mathrm{BCD}$ は2辺と挟角が等しく合同です．

一方 $\bigtriangleup \mathrm{BEA}$と $\bigtriangleup \mathrm{BEK}$は底辺が共通で高さが等しいので， 面積が等しいです．

同様に $\bigtriangleup \mathrm{BCD}$と $\bigtriangleup \mathrm{BHD}$も底辺が共通で高さが等しいので， 面積が等しいです．

よって，斜辺上の正方形を$\mathrm{CH}$によって2つに分けると， そのうちの一つの半分が， 辺$\mathrm{BC}$上の正方形の半分に等しいことが示せました．

辺$\mathrm{AC}$上の正方形についても同様です．

これで 直角三角形の各辺に，その辺を一辺とする正方形を作ると， 斜辺上の正方形の面積は，他の2つの辺上の正方形の面積の和に等しい， ことが示せました．　□

 

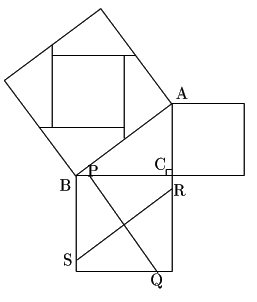
南海　 この定理から，次のようなこともわかる．

辺$\mathrm{BC}$上の正方形の各辺上に4点 $\mathrm{P},\ \mathrm{Q},\ \mathrm{R},\ \mathrm{S}$を， $\mathrm{PQ}$と$\mathrm{RS}$をたがいに直交し， かつ長さは斜辺$\mathrm{AB}$に等しくなるようにとる．

$\mathrm{PQ}$と$\mathrm{RS}$で四つに分けられた断片を， 斜辺上の正方形の直角にあわせて置く．

するとその真ん中にできる正方形が， 辺$\mathrm{AC}$を1辺とする正方形と同じ大きさになる．

美樹　 なぜ計量の基本が三平方の定理なのですか。

南海　 三平方の定理は何を主張しているのか．

美樹　 2つの正方形の面積の和が斜辺上の正方形の面積の和に等しい?

これは定理そのものですね．

南海　 三平方の定理は面積の関係でいわれるのだが， 長さの関係でいうとどのようになるのか．

美樹　 線分$\mathrm{AB}$の長さが

$$\mathrm{AB}=\sqrt{\mathrm{CA}^2+\mathrm{CB}^2}$$

となる．

南海　 そう． われわれの平面で普通に距離といっているものは， 2点 $\mathrm{A},\ \mathrm{B}$の間の距離$\mathrm{AB}$が， その2点を結ぶ線分を斜辺とするような直角三角形$\mathrm{ABC}$の， 直角を挟む2辺 $\mathrm{CA},\ \mathrm{CB}$の長さを用いて上のように表される．

三平方の定理はこれを主張している．

美樹　 長さが面積や体積の基本なので， 三平方の定理は計量の基本性質を定めているのですね．

$xy$平面上の2点 $\mathrm{A}(x_1,\ y_1),\ \mathrm{B}(x_2,\ y_2)$の間の距離が

$$\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$$

で与えられるというのも， 三平方の定理を根拠にしているのですね．

南海　 ところでこのことがわかったら，もう一息考えておこう．

原点を$\mathrm{O}$とする． 次の同値が成り立つ．

1. 2直線$\mathrm{OA}$と$\mathrm{OB}$が直交している．
2. $\mathrm{AB}^2=\mathrm{OA}^2+\mathrm{OB}^2$が成り立つ．
3. これを成分で書くと
   
   $$(x_1-x_2)^2+(y_1-y_2)^2={x_1}^2+{y_1}^2+{x_2}^2+{y_2}^2$$
4. 
   
   $$x_1x_2+y_1y_2=0$$

南海　 最後の式は，ベクトルでいうと $\overrightarrow{\mathrm{OA}}$と $\overrightarrow{\mathrm{OB}}$の内積が0 ということだ．

美樹　 高校では， $\overrightarrow{\mathrm{OP}}$と $\overrightarrow{\mathrm{OQ}}$の内積を，

$$\overrightarrow{\mathrm{OP}}\cdot\overrightarrow{\mathrm{OQ}... ...thrm{OP}}\vert\vert\overrightarrow{\mathrm{OQ}}\vert\cos\theta$$

で定め，そのうえで余弦定理によって

$$\overrightarrow{\mathrm{OP}}\cdot\overrightarrow{\mathrm{OQ}}= x_1x_2+y_1y_2$$

を示します．

南海　 そうだ． そのように教科書の理論構成の仕組みを考えておくことは大変いいことだ．

$xy$座標平面をベクトルの集合としてとらえることや， ベクトルの集合に内積を定めることと距離を定めることの同値性など， については， 『数学対話』の中の『線型代数の考え方』の「内積と直交変換」をみてほしい．

ここでは， 三平方の定理が長さを測ることの基礎である， ことを確認して，もう少し高校数学の仕組みをみていこう．

三平方の定理が成り立つような距離のことを 「ユークリッドの距離」(より正確には「ユークリッド計量」)という． 「ユークリッドの距離」が定まった平面をユークリッド平面という．

美樹　 ということは，他にも距離はあるのですか．

あっ，そういえば入試問題で， 2点 $\mathrm{P}(x_1,\ y_1),\ \mathrm{Q}(x_2,\ y_2)$に対して

$$d(\mathrm{P},\ \mathrm{Q})=\vert x_1-x_2\vert+\vert y_1-y_2\vert$$

とする，というのをみたことがあります．

これも距離ですか．

南海　 平面上の2点に対して負でない実数が定まるので，距離のようである．

これを距離と判断するためには， どんな性質を満たすものを距離というのか考えなければならない． つまり， 距離といえるためには，どのような条件が要請されるのか，考えていこう．

そのために，ユークリッドの距離ではどのような性質が成り立っているのか， それを調べよう．