次： 惑星の運動法則 上： 惑星の運動方程式を立てる 前： 惑星の運動方程式を立てる

運動法則の意義

南海　 ニュートンの第2法則は数学と物理学を結びつけている．

ベクトル $\overrightarrow{r}$や行列$A$の各成分が変数$t$の関数であるときに， 各成分を$t$で微分したベクトルや行列を $\dfrac{d}{dt}\overrightarrow{r}$や $\dfrac{d}{dt}A$と記す．

各成分を時間の関数とするベクトル $\overrightarrow{r}=(x(t),\ y(t),\ z(t))$を 位置を表すベクトルとする． 各成分を$t$で微分したベクトル $\dfrac{d}{dt}\overrightarrow{r}=(x'(t),\ y'(t),\ z'(t))$を 速度ベクトルという． 同様に，2次微分 $\dfrac{d^2}{dt^2}\overrightarrow{r}$も考えられる． それを加速度ベクトルという．これは数学の範囲にある量だ．

ところがこれが，その位置にある質点に働いた力と比例するというのだ． 「力」は物理量だ． 力もベクトルなのでこれを $\overrightarrow{F}$と記し，比例定数を$m$とすれば， ニュートンの第2法則は，

$$m\dfrac{d^2}{dt^2}\overrightarrow{r}=\overrightarrow{F}$$

となる． このように，未知関数 $\overrightarrow{r}$やその導関数が入った等式を微分方程式という． ニュートンの法則は，微分方程式として表される．

拓生　 この$m$は質量ですね．

南海　 というより，これが質量の定義式だ． 厳密には慣性質量という． これは物質に固有の量である．

拓生　 ところで，ニュートンの第1の慣性の法則ですが， 第2法則で力 $\overrightarrow{F}$を $\overrightarrow{0}$にすると， 加速度が0，つまり速度一定が出ませんか． なぜ，第1の法則を立てる必要があるのでしょうか．

南海　 第1の法則は，この世界を慣性系としてとらえようということだ． 慣性系であるから，例えば速度と質量を独立にとらえることが出来る． 慣性系でなければそもそも第2法則がそのままでは意味がない．

だから第2法則の前提として第1法則があるのであって，逆ではない．

拓生　 そういえば，第1の法則で「一様」ということがいわれます． しかしこれも，時間の客観的な存在を前提にしてはじめて意味ある言葉ではないでしょうか．

南海　 その通りである．第1法則は座標系とは独立した時間の存在をも宣言している．

さて， ニュートンが主著『自然哲学の数学的諸原理(プリンキピア)』(1687年7月5日)で示した もう一つの基本法則が，万有引力の法則だ．

拓生　 2つの物体の間には、互いに逆方向の引力が働き、その力 $\overrightarrow{F}$の大きさは， $G$を万有引力定数、物体の質量は$M,\ m$，物体間の距離を$d$とすると，

$$\vert\overrightarrow{F}\vert=\dfrac{GmM}{d^2}$$

となる．方向は2つの質点を結ぶ線に平行です． この方程式はベクトルでも表せます．右辺をベクトルで表すと， いずれを基準点にとるかで符号が逆になりますが，第3法則によって大きさは等しいです．

南海　 この式から定まる質量$m$と$M$が重力質量だ．

慣性質量と重力質量

拓生　 質量にいろいろあるのですか．

南海　 よく知られているように， ガリレオは「物の質量と落ちる速さとは関係がない」という落体の法則を発見した． このような否定形の法則は，その背後により大きな肯定形の原理をもつ． 「落体の法則」に関して言えば，それは一般相対論の「等価原理」である．

地球上でものを落とすと，その質量に関係なく$9.8m/s^2$で加速する．

では，地上で$1kg$の物質を無重力状態で毎秒$9.8m$の割合で加速させるには， どれだけの力が必要か？

拓生　 $1kg$の力です．

南海　 単位は正確に$kg\cdot m/s^2$といおう．これは普通$N$で表し「ニュートン」と呼んでいる．

ところで，加速度を与えるために必要な力が比例するのは物の「慣性質量」だ． 重力から受ける力は「重力質量」に比例する．

この2つを同一とみなすことが「一般相対性理論」の重要な前提である「等価原理」だ．

アインシュタインは， 1916年に「重力場のはたらきと， 座標系が慣性座標系にたいして加速度運動することによる見かけの力の場のはたらきが， すべての物理現象において同じはたらきをする」という 「等価原理」を一つの土台として， 「一般相対性理論」を発表した(もう一つの原理は「一般相対性原理」)．

「等価原理」によって，ある系にいる観測者は， 自分が，ある基準系にたいして加速度系にいるのか，重力場の中にいるのかがわからない．

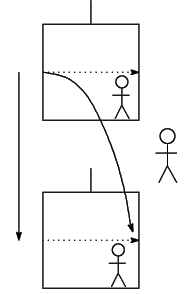落下するエレベーターの中の観測者に対してエレベータの中で光は直進するが， この光をエレベータの外の観測者から見れば，光は曲がって進んでいる． この，加速度系における思考実験によって，重力場によって光は曲げられることがわかる．

「等価原理」によって，重力とは空間の歪みであることが示される．

このことは，1919年5月29日，エディントン（Sir Arthur Stanly Eddington，1882〜1944）によって， 西アフリカのギニア湾，プリンレーベ島で，日蝕の際に検証された． つまり，地球から見て太陽の側にある星から出た光は太陽の重力場によってゆがめられるため， その見かけの位置が実際の位置からずれる． これをエディントンたちは検出したのである．

相対性理論によればこの世界はニュートンの意味での慣性系ではない． 慣性系であることは近似的にしか成り立たない． 速度はニュートンの慣性系ではいくらでも大きくなるはずだが， 相対性理論によれば，光速より大きな速度はない． 慣性の法則は近似法則なのである．