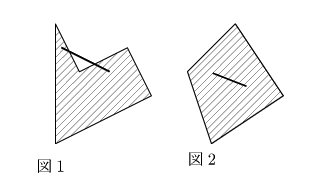
ここで二つの多角形を見てほしい.

結論からいうと図1は凸でない5角形だ.それに対して図2は凸な多角形だ.この違いを どのように定義するのか.
拓也 図を見せてもらったので気づきましたが,凸な方は内部の任意の2点を 結ぶ線分がまた内部にあるが,凸でないと,線分が外に飛び出すことがある.
南海 その通り.ここに「凸」をはっきりさせるカギがある.
以下で「多角形」とは,内部と周からなる ![]() 平面上の点の集合のこととする.
平面上の点の集合のこととする.
平面上の ![]() 角形
角形
![]() が「凸多角形」であるとは,この多角形の
任意の2点を結ぶ線分がつねにこの多角形に含まれることをいう.
が「凸多角形」であるとは,この多角形の
任意の2点を結ぶ線分がつねにこの多角形に含まれることをいう.
もちろん,この定義は凸多角形だけではなく,一般に「凸領域」の定義に拡張されるが, 今はそこまではいいだろう.
この概念をつかうと次の事実が成り立つ.
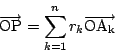
証明
必要条件を数学的帰納法で証明する.
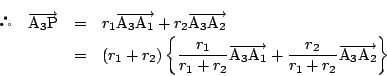
まず, ![]() 角形
角形
![]() が凸多角形なら
が凸多角形なら ![]() 角形
角形
![]() も凸多角形である.なぜなら点
も凸多角形である.なぜなら点 ![]() と
と ![]() を
を![]() 角形
角形
![]() の点とすると,
の点とすると,![]() 角形
角形
![]() が凸多角形なので,線分
が凸多角形なので,線分 ![]() は
は ![]() 角形
角形
![]() に含まれる.ところが
に含まれる.ところが![]() も
も![]() も直線
も直線
![]() に関して同じ側にあるので,線分
に関して同じ側にあるので,線分 ![]() も
直線
も
直線
![]() に関して同じ側にあり,したがって線分
に関して同じ側にあり,したがって線分 ![]() は
は ![]() 角形
角形
![]() に含まれるからである.
に含まれるからである.
ここで,実数
![]() を
を
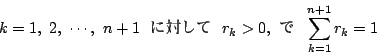
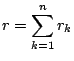 とおく.
とおく. 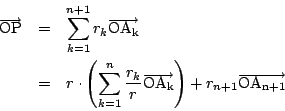
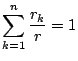 なので帰納法の仮定から
なので帰納法の仮定から
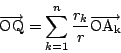
十分条件であることを示す.
![]() 角形
角形
![]() の2点
の2点 ![]() ,
,![]() と
実数
と
実数 ![]() に対して
に対して
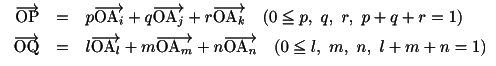
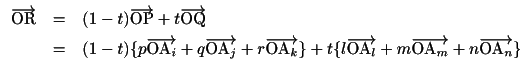
拓也 なるほど.これで気づいたのですが,三角形はつねに「凸」なのですね.
南海 そうなのだ.4角形からはつねに凸というわけではない.