[79鹿児島大]
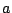 を与えられた正の定数とするとき,
を与えられた正の定数とするとき,
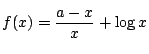 の最小値を求めよ.ただし,
の最小値を求めよ.ただし, 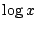 は
は 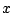 の自然対数を表すものとする.
の自然対数を表すものとする.
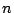 個の関数
個の関数
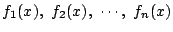 と
それらの和
と
それらの和
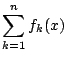 がいづれも最小値をもつとき,
それらの最小値を,それぞれ,
がいづれも最小値をもつとき,
それらの最小値を,それぞれ,
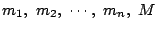 とすると,
とすると,
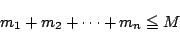
となることを示せ.- 上の結果を利用して
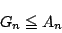
を示せ.また,この不等式で等号が成立する場合を吟味せよ.
まず97年に鹿児島大学で出題されたものを紹介しよう. 雜誌『初等数学』(2001年3月号)の宮地俊彦先生によるともともと宮地先生がどこかで 話されたものが鹿児島大の先生の耳に入り入試問題になったそうだ.ちなみにできは 非常に悪かったそうである.
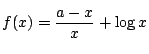 の最小値を求めよ.ただし,
の最小値を求めよ.ただし, 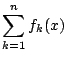 がいづれも最小値をもつとき,
それらの最小値を,それぞれ,
がいづれも最小値をもつとき,
それらの最小値を,それぞれ,
解
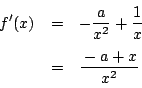
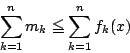
一方,和
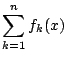 が
が ![]() で最小値
で最小値![]() をとるとすると,
をとるとすると,
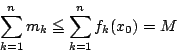
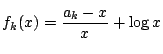 とおく.これは
とおく.これは
一方
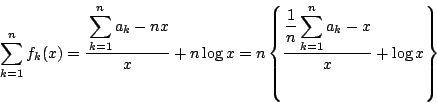
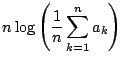 である.
したがって(1)から
である.
したがって(1)から
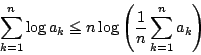
また別のものが 00年滋賀県立大で出題された.昔から知られている方法である.
解
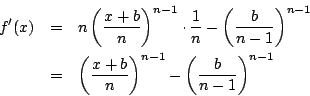
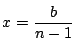 で極小かつ最小である.つまり
で極小かつ最小である.つまり
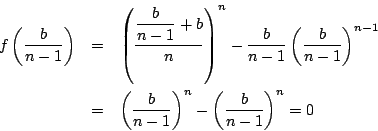
![]() のときより
のときより![]() が正の実数で
が正の実数で ![]() が2以上の自然数のとき,不等式
が2以上の自然数のとき,不等式
![]() のとき(1)の結論から
のとき(1)の結論から
![]() で成立するとする.
で成立するとする.
![]() ,
,
![]() ,
, ![]() で(1)の結論を用いると
で(1)の結論を用いると
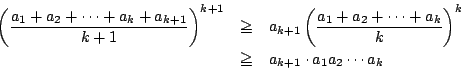
したがって ![]() の自然数について
の自然数について
さらに,これはやったことがあるかも知れない.
解
![\begin{eqnarray*}
{f_n}'(x)
&=&\dfrac{1}{n}-\sqrt[n]{A}\cdot\dfrac{1}{n}x^{ \f...
...{n}-1}\\
&=&\dfrac{1}{n}(1-A^{ \frac{1}{n}}x^{\frac{1-n}{n}})
\end{eqnarray*}](images/img422.png)
最小値は
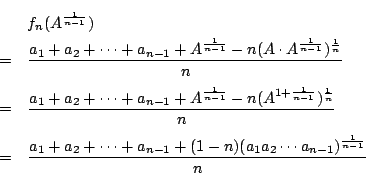
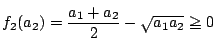 .
つまり
.
つまり
(1)の最小値を ![]() で用いて
で用いて
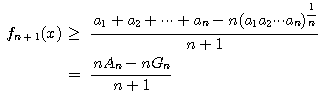
ゆえに,帰納法の仮定から 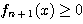 である.
である.
次のものは凸関数を用いる証明[2]と本質的には同じなのだが, 相加平均,相乗平均の大小関係の証明に特化することでより簡単にできる. 二つの方法をまとめてある.雜誌『初等数学』(1999年8月号)の宮地俊彦先生の報告による.
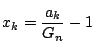 とおけ.得られた不等式を
すべて加えることで
とおけ.得られた不等式を
すべて加えることで
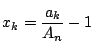 とおけ.得られた不等式を
すべて加えることで
とおけ.得られた不等式を
すべて加えることで
解
![]() なので
なので ![]() で,等号成立は
で,等号成立は ![]() のときのみ
であることが示された.
のときのみ
であることが示された.
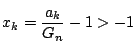 である. (1)から
である. (1)から
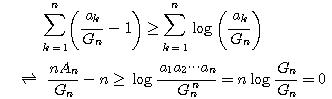
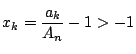 なので(1)が使える.
なので(1)が使える.
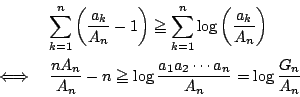
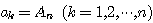 のときに限る.
これは
のときに限る.
これは