![]() または
または ![]() からなる数列
からなる数列
![]() において,
そのうち
において,
そのうち ![]() 個が
個が ![]() で,
で, ![]() 個が
個が ![]() とする.
とする.
![]() に対し
に対し
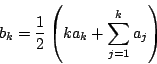
とおく.集合
を求めよ.
例を用いて考えることで,実はそこで成立している型(パターン)を認識することができる.それを記述すればそれが解答になる. 例によって型の認識を助け,それを引き出すことができるのである. 個別から一般へ,これが例で考えるということである. 例で考えよう!
例題 2.16 [01京大文系後期]
![]() または
または ![]() からなる数列
からなる数列
![]() において,
そのうち
において,
そのうち ![]() 個が
個が ![]() で,
で, ![]() 個が
個が ![]() とする.
とする.
![]() に対し
に対し
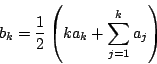
考え方
これは一体なんだ! というのが正直なところだ.
そこで例を2,3作って考える. ![]() で考えよう.
ここでまず条件を満たす数列はいくつもあることに気づく.
で考えよう.
ここでまず条件を満たす数列はいくつもあることに気づく.

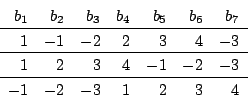
いろんな抽象的な問題で例を作って考える大切さを認識してもらいたい.
さて,推測できた段階で次に進む.本例題の証明方法はいろいろある.
ここでは,作った例から問題の仕組みを考え, より直接的に証明する方法でやってみよう.
例を見てみると, ![]() は
は
![]() のうちの1の個数か,
のうちの1の個数か,
![]() の個数に
の個数に![]() をかけたものになっていることに気づく.
そこでもう一度
をかけたものになっていることに気づく.
そこでもう一度 ![]() の作り方をよく見てみよう.
の作り方をよく見てみよう.
![]() の
の![]() 倍と,
倍と, ![]() 個の和の和!
個の和の和!
解1
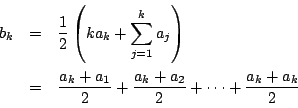
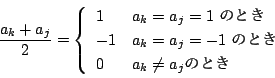
したがって ![]() は
は
![]() の中にある
の中にある![]() と同じものの個数と
と同じものの個数と![]() をかけあわせた値に一致する.
1と同じものの個数と
をかけあわせた値に一致する.
1と同じものの個数と![]() をかけあわせた値は順に
をかけあわせた値は順に
![]() であり,
であり,
![]() と同じものの個数と
と同じものの個数と![]() をかけあわせた値は順に
をかけあわせた値は順に
![]() である.
である.
![]() はこれらの値を1回ずつとる.したがって
はこれらの値を1回ずつとる.したがって