

 次: 変形型数学的帰納法
上: 論証の推進
前: 考え方
次: 変形型数学的帰納法
上: 論証の推進
前: 考え方
「数学的帰納法」はよく知っている言葉だが,
ではその中にある「帰納」とはどういう意味なのだろうか.
「帰納」は「演繹」という言葉と対になっている.
「帰納」とは多くの例を調べその間になり立つ法則を推測して
きっとこうに違いなという「仮説」を立てることだ.
「演繹」は,成立することがわかっている一般的な命題をもとに,
具体的,個別的な命題を推論によって証明することをいう.
では「数学的帰納法」とは何か.
自然数を含む数学的事柄がどのようになっているかを知りたいとき,
- (1)
- 1のときはこうだ,2のときはこうだと調べていって
- (2)
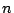 のときもこうに違いないと推測して仮説を立て,
のときもこうに違いないと推測して仮説を立て,
- (3)
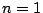 で成立する.
で成立する.
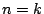 で成立すれば
で成立すれば 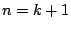 でも成立する.
ゆえに任意の
でも成立する.
ゆえに任意の 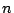 で成立することを証明する.
で成立することを証明する.
というのが普通のやり方だ.
この(3)の部分の証明方法のことが「数学的帰納法」である.
このような証明法が可能な根拠は自然数の次の性質による.
自然数の部分集合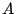 が次の性質をもっているとする.
が次の性質をもっているとする.
このとき集合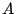 は自然数の集合
は自然数の集合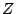 と一致する.
と一致する.
数学的帰納法では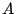 は命題の成立する番号の集合である.
は命題の成立する番号の集合である.
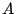 が上の性質が成り立つことを示すことで,
が上の性質が成り立つことを示すことで,
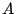 が自然数の全体に一致し,
したがってすべての自然数でその命題が成立する,
これが数学的帰納法の原理だ.
が自然数の全体に一致し,
したがってすべての自然数でその命題が成立する,
これが数学的帰納法の原理だ.
入試問題では,(1)〜(3)全体が問題になることもあれば,
仮説は提示して(3)の部分の論証だけが問題になることもある.
この(3)の部分の証明法は,この通りの形である必要はなく,
いくつかの応用形がある.まずそれを確認しよう.
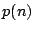 を自然数
を自然数 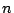 に関する条件とする.
に関する条件とする.
「すべての自然数 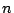 に対し条件
に対し条件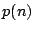 が成立する」
ことを証明する方法としての数学的帰納法の主な型は次の三つである.
が成立する」
ことを証明する方法としての数学的帰納法の主な型は次の三つである.
- [基本型]
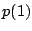 が成立する.
が成立する.
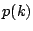 が成立するなら
が成立するなら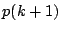 が成立する.
が成立する.
- (1), (2)より, すべての
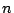 に対して
に対して 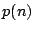 が成立する.
が成立する.
- [応用型1]
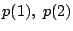 が成立する.
が成立する.
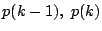 が成立するならば
が成立するならば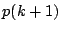 が成立する.
が成立する.
- (1), (2)より, すべての
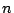 に対して
に対して 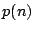 が成立する.
が成立する.
- [応用型2]
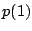 が成立する.
が成立する.
-
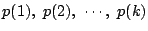 が成立するなら
が成立するなら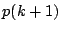 が成立する.
が成立する.
- (1), (2)より, すべての
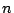 に対して
に対して 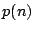 が成立する.
が成立する.
いずれの型で証明しようとしているのか,はっきりさせて論述しなければならない.
Aozora Gakuen
が次の性質をもっているとする.
は自然数の集合
と一致する.
![]() を自然数
を自然数 ![]() に関する条件とする.
に関する条件とする.
![]() に対し条件
に対し条件![]() が成立する」
ことを証明する方法としての数学的帰納法の主な型は次の三つである.
が成立する」
ことを証明する方法としての数学的帰納法の主な型は次の三つである.