

 次: 対偶を示す
上: 論証の推進
前: 考え方
間接証明というのは広い概念である.
命題
次: 対偶を示す
上: 論証の推進
前: 考え方
間接証明というのは広い概念である.
命題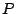 が成立することを示すのに,
直接
が成立することを示すのに,
直接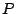 の成立を示すのではなく,
「このような理由で
の成立を示すのではなく,
「このような理由で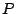 が成立する以外にありえない」
ということを示すのである.
多くの場合,根拠になっているのは排中律,つまり命題
が成立する以外にありえない」
ということを示すのである.
多くの場合,根拠になっているのは排中律,つまり命題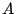 か
その否定
か
その否定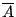 のいずれか一方がつねに成立し,
のいずれか一方がつねに成立し,
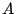 でもなければ
でもなければ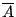 でもないという第三の場合はない,
ということである.
でもないという第三の場合はない,
ということである.
代表的な間接証明は対偶証明と背理法である.
命題:「 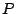 ならば
ならば 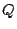 である」の真偽と,
その対偶命題:「
である」の真偽と,
その対偶命題:「 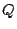 でなければ
でなければ 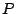 でない」の真偽は一致する.
したっがて[
でない」の真偽は一致する.
したっがて[ 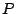 ならば
ならば 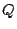 ]を証明するためには
[
]を証明するためには
[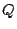 でなければ
でなければ 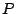 でない]を証明すればよい.
対偶が成立することを示すことで,もとの命題が成立することを示す証明は,
直接に[
でない]を証明すればよい.
対偶が成立することを示すことで,もとの命題が成立することを示す証明は,
直接に[ 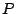 ならば
ならば 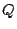 ]を証明するのではないから間接証明の一つである.
]を証明するのではないから間接証明の一つである.
この対偶を用いた証明法の応用として背理法がある.
「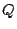 でないと仮定する.すると前提条件
でないと仮定する.すると前提条件 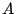 と矛盾が起こる.したがって
と矛盾が起こる.したがって 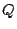 が成立する.」
このような証明法を 背理法という.
が成立する.」
このような証明法を 背理法という.
しかし背理法は「対偶による証明」より応用が広い.
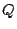 を示したい,しかし明示的には
を示したい,しかし明示的には 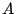 が書かれていない.
このようなときにも
が書かれていない.
このようなときにも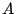 を適切にとって何らかの矛盾に持ち込めばいいからだ.
を適切にとって何らかの矛盾に持ち込めばいいからだ.
対象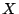 が条件
が条件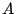 を満たし,対象
を満たし,対象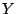 も条件
も条件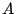 を満たす.
かつ条件
を満たす.
かつ条件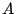 を満たすものはただ一つに定まる.
ゆえに
を満たすものはただ一つに定まる.
ゆえに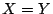 である.
である.
これも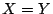 を直接に示すのではないので,
間接証明である.
を直接に示すのではないので,
間接証明である.
その他,「存在の証明」で扱う「鳩の巣原理」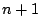 個以上のボールのそれぞれが
個以上のボールのそれぞれが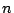 個の箱のいずれかに入っている.2個以上のボールが入っているはこが存在する.」
個の箱のいずれかに入っている.2個以上のボールが入っているはこが存在する.」
あるいは数学的帰納法も間接証明であるし,
ある命題
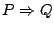 が偽であることを示すのに,反例:
が偽であることを示すのに,反例: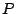 であって
であって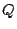 ではない例をあげるのも間接証明である.
ではない例をあげるのも間接証明である.
Aozora Gakuen
![]() を示したい,しかし明示的には
を示したい,しかし明示的には ![]() が書かれていない.
このようなときにも
が書かれていない.
このようなときにも![]() を適切にとって何らかの矛盾に持ち込めばいいからだ.
を適切にとって何らかの矛盾に持ち込めばいいからだ.
![]() を直接に示すのではないので,
間接証明である.
を直接に示すのではないので,
間接証明である.
![]() 個以上のボールのそれぞれが
個以上のボールのそれぞれが![]() 個の箱のいずれかに入っている.2個以上のボールが入っているはこが存在する.」
個の箱のいずれかに入っている.2個以上のボールが入っているはこが存在する.」
![]() が偽であることを示すのに,反例:
が偽であることを示すのに,反例:![]() であって
であって![]() ではない例をあげるのも間接証明である.
ではない例をあげるのも間接証明である.