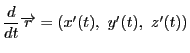 を
速度ベクトルという.
同様に,二次微分
を
速度ベクトルという.
同様に,二次微分
このようにして準備された数学は,物理現象を近似してとらえる.とらえられた現象は数学の言葉をもって記述される.いくつかの基本的な物理現象の性質は,物理法則といわれる.これまで準備した数学では,ニュートン力学を記述し,その基本法則から演繹的に,いくつかの物理現象が起こる根拠を解明することができる.
これまで数学として準備してきたことをもとに,ニュートンが万有引力の法則からケプラーの法則を導いた内容を,再構成してみよう.
ベクトル
![]() や行列
や行列![]() の各成分が変数
の各成分が変数![]() の関数であるときに,
各成分を
の関数であるときに,
各成分を![]() で微分したベクトルや行列を
で微分したベクトルや行列を
![]() や
や
![]() と記す.
各成分を時間の関数とするベクトル
と記す.
各成分を時間の関数とするベクトル
![]() を
位置を表すベクトルとする.
各成分を
を
位置を表すベクトルとする.
各成分を![]() で微分したベクトル
で微分したベクトル
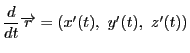 を
速度ベクトルという.
同様に,二次微分
を
速度ベクトルという.
同様に,二次微分
![]() も考えられる.
それを加速度ベクトルという.これは数学の範囲にある量である.
これがその位置にある質点に働いた力と比例するというのが第二法則である.
「力」は物理量だ.
力もベクトルなのでこれを
も考えられる.
それを加速度ベクトルという.これは数学の範囲にある量である.
これがその位置にある質点に働いた力と比例するというのが第二法則である.
「力」は物理量だ.
力もベクトルなのでこれを
![]() と記し,比例定数を
と記し,比例定数を![]() とすれば,
ニュートンの第二法則は,
とすれば,
ニュートンの第二法則は,
数学的には第一の慣性の法則は第二法則から出る.
第二法則で加わる力
![]() を
を
![]() にすると,加速度が0,つまり速度一定が出る.
ではなぜ第一の法則を立てる必要があるのか.
それは,第一の法則は,この世界を慣性系としてとらえるということの宣言だからである,慣性系であるから,例えば速度と質量を独立にとらえることが出来る.慣性系でなければそもそも第二法則がそのままでは意味がない.
だから第二法則の前提として第一法則があるのであって,逆ではない.
にすると,加速度が0,つまり速度一定が出る.
ではなぜ第一の法則を立てる必要があるのか.
それは,第一の法則は,この世界を慣性系としてとらえるということの宣言だからである,慣性系であるから,例えば速度と質量を独立にとらえることが出来る.慣性系でなければそもそも第二法則がそのままでは意味がない.
だから第二法則の前提として第一法則があるのであって,逆ではない.
また第一の法則で「一様」といわれる. これは時間の客観的な存在を前提にしてはじめて意味ある言葉である. つまりニュートンの法則にはその前提として絶対空間と絶対時間がある. 第二法則は座標系とは独立した時間の存在をも宣言している.
このように自然現象をとらえる枠組をニュートンは提示した. この枠組でとらえられた物理学がニュートン力学である. このような枠組は, ニュートンが主著『自然哲学の数学的諸原理(プリンキピア)』(1687年7月5日)で示した.
二つの物体の間には、互いに逆方向の引力が働き、その力の大きさは,
を万有引力定数、物体の質量は
,物体間の距離を
とすると,
となる.方向は二つの質点を結ぶ線に平行である.この式から定まる質量
この辺りの歴史的事実, あるいは慣性質量と重力質量などについては『数学対話』「惑星は楕円軌道を描く」を見てほしい.
ケプラーは三つの法則をいちどに発見したのではない. まず面積速度が一定であることを発見した. そこから,天体の運行には何らかの法則があることを知り,その内容をさらに追求した. そしてついに,惑星の軌道を楕円と仮定すると, 観測結果を説明できることが分かった.
ニュートンは,月をその軌道に保つのに必要な力と地表面上の重力を比較してみた. その結果,きわめてよい近似で満足な結果が得られた. こうしてニュートンはケプラーの法則から万有引力の法則を導き出した. がそれに留まらず,ニュートンの法則と万有引力の法則のもとでは, ケプラーの法則が導き出されることを示した.
次のような例でも,物理法則の表現が局所的なものと大域的なものの二通りあることがわかる. このように法則を数学的に把握することは, 歴史的には,ガリレオの研究がはじまりである.
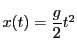 となることを得た.
彼は条件
となることを得た.
彼は条件
力学の発展によって,これはさらに落下する物体の加速度が一定であるととらえられた.
自然界の同じ法則が,一つは微分の形で,一つは具体的な関数の形で表された.
微分方程式で表された法則を微分法則という.
これは局所的な法則が一定の範囲で成り立つことを表している.
それに対して,それを解いて得られた![]() は各時刻における物質量を明示的に表している.
このように表された法則を積分法則という.このような命名はアインシュタインによる.
例8.1よりはもちろん精密にしなければならないが,
ニュートンの法則の下でケプラーの法則という積分法則から
万有引力の法則という微分法則が導き出される.
は各時刻における物質量を明示的に表している.
このように表された法則を積分法則という.このような命名はアインシュタインによる.
例8.1よりはもちろん精密にしなければならないが,
ニュートンの法則の下でケプラーの法則という積分法則から
万有引力の法則という微分法則が導き出される.
逆に,万有引力の法則が成り立つならケプラーの法則が成り立つことが示される. 「太陽と惑星の間に距離の二乗に反比例する引力が働く」という微分法則が成り立つとき, これを満たす関数を位置関数決定することによって, 「ケプラーの三法則」という積分法則を満たすことが示される. ニュートンはこの間題を解決し,彼の主著「プリンキピア」(1687)でその解法を公表した. その過程で,微分法,積分法が開始された. このように解析学は微分方程式を解いて自然現象を解明するところからはじまった. これは本質的に微分方程式を解いて,積分法則を導くことであり, 実質的にニュートンがはじめておこなったことである. この過程を,これまで準備したことをもとに追体験することが最後の目的である.