001k

静岡大解説　　　問題に戻る　　 2000年入試に戻る

この問題の基本は連立漸化式と3項間漸化式の同値性にかんする理論である.
静岡大の問題は，3項間漸化式を解くことで行列のn 乗を求めようとしているのだが,大切なことは,同値性だ.

　この定理が次のように連立漸化式と3項間漸化式を結びつける.

連立漸化式と3項間漸化式と2次行列

数列 $\{ x_n \}$ と $\{ y_n \}$ の連立漸化式

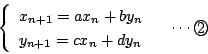
$\begin{displaymath}\left\{ \begin{array}{l} x_{n+1}=a x_n+by_n\\ y_{n+1}=c x_n+dy_n \end{array}\right. \quad \cdots \maru{2} \end{displaymath}$

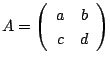を考えよう．行列 $A=\matrix{ a}{b}{c}{d}$ を考えるとこの連立漸化式は

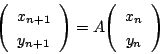
$\begin{displaymath}\vecarray{x_{n+1}}{y_{n+1}}=A\vecarray{x_n}{y_n} \end{displaymath}$

となる．したがって，等比数列と同様に

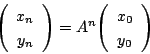
$\begin{displaymath}\vecarray{x_n}{y_n}=A^n\vecarray{x_0}{y_0} \end{displaymath}$

となる．だから Aⁿ が求まれば，数列 $\{ x_n \}$ と $\{ y_n \}$ の一般項が求まる．
　ハミルトン・ケイレイの定理より，

A ²-(a+d)A + (ad-bc)E = 0

つまり

$\begin{displaymath}A^{n+2}-(a+d)A^{n+1}+(ad-bc)A^n=0 \quad \cdots \maru{3} \end{displaymath}$

である．

　これから A ⁿ を求める過程は，三項間漸化式を解くのとまったく変わらない.

　これからまた

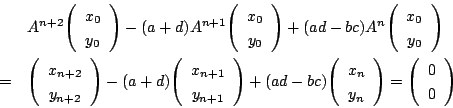
$\begin{eqnarray*}&&A^{n+2}\vecarray{x_0}{y_0}-(a+d)A^{n+1}\vecarray{x_0}{y_0}+(a... ...ray{x_{n+1}}{y_{n+1}}+(ad-bc)\vecarray{x_n}{y_n}=\vecarray{0}{0} \end{eqnarray*}$

である. つまり，数列 $\{ x_n \}$ と $\{ y_n \}$ はともに同じ3項間漸化式を満たす．

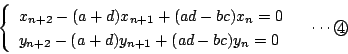
$\begin{displaymath}\left\{ \begin{array}{l} x_{n+2}-(a+d)x_{n+1}+(ad-bc)x_n=0\... ...y_{n+1}+(ad-bc)y_n=0 \end{array}\right. \quad \cdots \maru{4} \end{displaymath}$

　A ⁿ を求めることと，この3項間漸化を解くのが同値である.

　なお, これらの3項間の関係式から一般項を求めることは通常の解き方で解けるが,もう少し簡便にもできる．

　つまり

このとき

となる.ここでも用いられたのはケイレイハミルトンの定理である.

である.

$t^2-(a+d)t+(ad-bc)=(t-\alpha)(t-\beta)$ とおいて p_nt + q_n を求め，これまでの3項間漸化式の解き方で解いたものと比較しておいてほしい．