横浜国大経済2　解答　問題に戻る　2000年入試に戻る

数列 ｛a_n}  に対して形式的においた無限級数

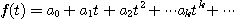
を数列 ｛a_n}  の生成関数という.　漸化式の関係から，生成関数と他のよくわかった関数との関係を導き，それによって関数 f(t) を求めれば，　その点開式の係数から数列 ｛a_n} 　が求まるのだ.．

よくわかった関数として今は

を用いた.．

もちろん，これらの無限級数は本当に収束するのか，　ということが気になるところだ.．下の無限等比級数は

で収束するし，　あとで現れたもう一つの無限等比級数も

で収束する.　だからそれらと一定の関係を持つ f(t) もこの範囲で収束する．

　だから始めに「十分小さい t 」としておいたのだ.．　だがさらにいえば，生成関数の方法は，形式的な無限次数の多項式全体のなかで恒等的に成り立つ関係から係数比較をするもので，収束性は気にしなくても数列を確定してよい.

　たいへん強力な方法なので，いろいろやってみるとおもしろい.