No Title

東大理 I 後期総合科目II 2　解答　解説　 2001年入試に戻る

　スーパーコンピュータは超高速の処理能力をもっコンピュータで，大学のコンピュ‐タセンターなどに置かれ，主に科挙技術計算に使用される．ここでは，ネットワークにつながれ，多数のユーザーが利用するスーパーコンピュータの動作を考えよう．ユーザーはスーパーコンピュータで処理するプログラム (ジョブと呼ぶ)をネットワークを介して送り，スーパーコンピュータは受け付けた順にひとつずつそれらを処理する．

　まず，ジョブの受け付けを考えよう．多数の利用者からあるスーパーコンピュータにジョブがランダムに到着するものとする．ランダムに到着とは，微小時間 ${\it\Delta}t$ の間にジョブが到着する確率を，正の定数 $\lambda$ を用いて $\lambda{\it\Delta}t$ と表せることである．このとき，ある時間間隔 t の間にジョブが到着しない確率が $e^{-\lambda t}$ となることを次の手順で示せ．

1 ${\it\Delta}t$ の間にジョブが到着しない確率を索めよ．

2 E(t)と $E(t+{\it\Delta}t)$ の関係を表せ．

3 2 で求めた式の ${\it\Delta}t \to 0$ の極限をとり， $\dfrac{dE(t)}{dt}$ を求め，その式を E(0)=1の条件で解け．

　次に，スーパーコンピュータでのひとつのジョブの処理を考える．ジョブには，処理に要する時間が短いものも長いものもさまざまある．ここでは，ジョブの処理時間のばらつきについて，処理が開始されてからジョブが終了するまでに要する時間はランダムであるとする．つまり，処理の行われているジョブが微小時間 ${\it\Delta}t$ の間に終了する確率を $\mu {\it\Delta}t$ とし， $\mu$ は正の定数とする．このとき，処理が開始されてから時間 t が経過するまでの間にそのジョブが終了しない確率F(t)はAと同様に $e^{-\mu t}$ となる．ここで

4 時間 t が経過するまでの間にジョブが終了する確率G(t)を求め，それを横軸 t に対して図示せよ．

5 次に，ジョブの処理時間が確率的にどのように分布しているかを考えよう．ジョブの処理時間が T である確率をH(T)という関数で表す．ここでH(T)を T について0から t まで積分したものがG(t)であることを利用してH(T)を求め，それを横軸 T に対して図示せよ．

6 H(T)から，ひとつのジョプの処理時間の平均を求めよ．

　さて.ジョブはスーパーコンピュータに到着すると処理に移される．前に到着たジョブの処理が終了する前に次のジョブが到着すると，そのジョブは前のジョブが終了するまで侍たされ，前のジョブの終了後に処理が開始される．ジョプの処理はひとずつ行われるものとし，複数のジョブの並列処理は考えない．
　ここで，ジョブの到着とジョブ処理時間のぱらっきは上のA，Bと同一の条件であるとし，定数 $\lambda,\ \mu$ を用いるものとする．ある時刻 t において処理が実行中のものと侍っているものを合わせ n 個のジョブが蓄えられている確率をP_n(t)とする．ジョブがひとつ到着すれぼ n は1増加し，ひとつ処理されれぱ n は1減少する．

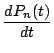7 微小時間 ${\it\Delta}t$ の間の変化を考え， $n\ge 1$ に対して， $P_n(t+{\it\Delta}t)$ を $P_{n-1}(t),\ P_n(t),\ P_{n+1}(t)$ で表せ．この式の ${\it\Delta}t \to 0$ の極限をとり， $\dfrac{dP_n(t)}{dt}$ を $P_{n-1}(t),\ P_n(t),\ P_{n+1}(t)$ で表せ．

8 同様のことを n=0 について考え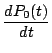， $\dfrac{dP_0(t)}{dt}$ を $P_0(t),\ P_1(t)$ で表せ．

9 さて，ここで $P_n(t)\ (n=0,\ 1,\ 2,\ \cdots)$ が時間の推移に対してその統計的性質が変化しない定常状態になったものとし， P_n(t)=p_nと書くこととする．これを定常確率過程という．このとき $\dfrac{\lambda}{\mu}=k$ として $p_1,\ p_2$ および p_nをp₀で表せ．ここで k<1 とする．

10 $p_0+p_1+\cdots+p_n+…=1$ の条件を用いてp₀，すなわちジョブがすぐに受け入れられる確率を求めよ．

11 待っているジョブの数の期待値を求めよ．