東大文系前期2 解答 解説 2001年入試に戻る
時刻 0 に原点を出発した2点 A,B が xy 平面上を動く.点 A の時刻 t での座標
は 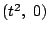 で与えられる.点 B は,最初は y 軸上を y 座標が増加する方向に一定の
速さ 1 で動くが,点C
で与えられる.点 B は,最初は y 軸上を y 座標が増加する方向に一定の
速さ 1 で動くが,点C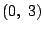 に到達した後は,その点から x 軸に平行な直線上を x
座標が増加する方向に同じ遠さ 1 で動く.
に到達した後は,その点から x 軸に平行な直線上を x
座標が増加する方向に同じ遠さ 1 で動く.
t>0 のとき 三角形ABCの面積を S(t) とおく.
-
- (1)
関数
のグラフの概形を描け.
- (2)
u を正の実数とするとき.
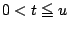 におけるS(t)の最大値をM(u)とお
く.関数
におけるS(t)の最大値をM(u)とお
く.関数
のグラフの概形を描け.